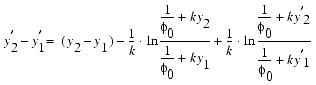SAMPLES AND METHODOLOGY
It was originally intended that the quantification of data would be undertaken mainly by microscope examination and point counting using the smear slides prepared shipboard. However, poor sorting of the sediments and the large proportion of grains less than 30 µm in diameter meant that normal petrographic techniques could not be employed. In addition, as we believed it important to examine the siliciclastic grain-size distribution, core plugs of sediment samples were required. Accordingly, we obtained sediment samples (see below), each of which was split into four subsamples on the basis of grain size. X-ray diffraction (XRD) analysis was used to quantify the mineralogy of the entire sample and of each grain-size split individually. The details of sampling procedure, preparation, and analysis are given below.
Subsamples of ~3-5 cm3 (~5-10 g) were obtained from 20 cm3 samples collected shipboard for microfabric study. Subsampling was undertaken at the University of Hawaii in May 1996. The original 20-cm3 sample suite had been collected at a rate of one per core from the working-half split and stored in sealed plastic bags at a temperature of ~3°C. The subsample set used in this study was collected using a clean stainless steel spatula and was stored in sealable cylindrical plastic tubes that had previously been oven dried at 60°C, cooled in a desiccator, and weighed. The open tubes were covered with permeable plastic wrap, frozen to -25°C, and freeze dried. After warming to ambient temperature in a desiccator, the tube and sample were weighed to determine sample mass. One hundred and sixty samples were taken to Australia in sealed tubes for the remainder of the study.
Sediment texture was determined by wet sieving and weighing of individual sample splits (Table
1). Between 2 and 6.5 g of each sample was weighed on glossy paper using a Shimadzu electronic balance, brushed into a 100-ml sealed plastic container, and suspended in ~20-30 ml distilled water by vigorous shaking. Samples were split into four grain-size divisions by wet sieving using three 100-mm-diameter sieves with mesh sizes of 63 µm, 32 µm, and 20 µm, stacked over a l-L glass beaker. This gave four grain-size divisions, >63 µm (sand), 63-32 µm (coarse silt), <32-20 µm (mostly medium silt) and <20 µm (fine silt and clay). Sediment was washed through the sieve stack with additional distilled water as required. Gentle agitation was required to break up some aggregates. The three sieve fractions were oven dried in the sieve at 60°C, retrieved by fine brushing onto glossy paper, placed into previously dried and weighed glass vials, and weighed. The <20-µm fraction was centrifuged at 6000 rpm in a Sorvall Superspeed Centrifuge to reduce water content before oven drying in a previously dried and weighed glass Petrie dish. The <20-µm fraction from Holes 976B and 977A was brushed from the glass Petrie dish onto glossy paper and then sealed into previously dried and weighed glass vials, before weight determination. Total average recovery from the sieving process by this method was 93.4% for the two holes. For Holes 978A and 979A, the proportion of the <20-µm fraction was determined by weight difference (original sample less [>63 µm] + [63-32 µm] + [32-20 µm] fractions) assuming the above recovery rate, to speed up sample recovery. Sieves were cleaned in a sonic bath after each sample run and then rinsed in distilled water. All glass, plastic, and metal ware were washed and rinsed in distilled water between the splitting of each sample.
XRD data were collected using a Siemens D5000 X-ray diffractometer setup in  -
- configuration and housed at the Microstructural Analysis Unit at the University of Technology, Sydney. The X-ray source was a long-fine focus copper anode tube emitting X-rays at 1.540562 Å for k
configuration and housed at the Microstructural Analysis Unit at the University of Technology, Sydney. The X-ray source was a long-fine focus copper anode tube emitting X-rays at 1.540562 Å for k 1 and 1.544390 Å for k
1 and 1.544390 Å for k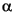 2. Data measurements were made from 2°2
2. Data measurements were made from 2°2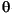 to 70°2
to 70°2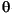 at increments of 0.02°2
at increments of 0.02°2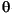 . XRD data were collected for each unsorted sample and for each of the four split fractions. Because of the small sample volume in each grade fraction, all samples were dry sedimented onto 25 x 37.5 mm glass slides, dispersed in distilled water, and dried at 60°C. The >63-µm fractions were ground using a mortar and pestle, before being placed on the glass slides.
. XRD data were collected for each unsorted sample and for each of the four split fractions. Because of the small sample volume in each grade fraction, all samples were dry sedimented onto 25 x 37.5 mm glass slides, dispersed in distilled water, and dried at 60°C. The >63-µm fractions were ground using a mortar and pestle, before being placed on the glass slides.
Quantification of XRD Data
Mineral proportions were calculated using SIROQUANT, a commercially available MS-Windows program for standardless mineral quantification. The software uses up to 15 operator-selected mineral phases, chosen from an included data bank, to calculate a theoretical XRD intensity profile that is then fitted to the measured profile by refinement of the Rietveld parameters. The majority of samples studied here were analyzed using 13 mineral phases (i.e., quartz, albite, bytownite, orthoclase, chlorite, illite, kaolinite, muscovite, talc, halite, pyrite, dolomite, and calcite). Gypsum was additionally present in a few samples and was added to the control (= task) file for their analysis. These minerals fit most of the major crystal peaks represented on the XRD data, and the presence of most was confirmed from other sources. These were (1) quartz, calcareous microfossils, muscovite, and pyrite, which were chosen because they are visible in smear slides, and dolomite, which was identified shipboard by XRD analysis; (2) feldspars, which were also recognized in smear-slide examination, and albite, bytownite, and orthoclase were chosen as representative of the group; (3) halite, which was included because the sediments were deposited in a marine environment; and (4) the four phyllosilicate minerals, which were selected because of the presence of strong primary peaks in the XRD data that most closely corresponded to standard patterns for these particular minerals. Unoriented hkl files were used for all phases except the clays, for which hkl files oriented on the 001 face and multiples were created and used because of the method of sample preparation.
The above mineral suite was not entirely satisfactory, particularly with respect to the clay minerals, but as these were not the primary focus of the study, refinement of identification was not pursued in this study. The principle difference between samples was the variable d-spacing represented by the peaks between 6°2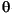 and 13°2
and 13°2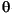 . In particular, the peak representing a lattice d-spacing of 14.2Å, interpreted to be an oriented 001 chlorite peak, varies between 14.40 and 14.04Å. Similarly the muscovite 002, talc 002, and kaolinite 001 peaks, represented by high intensities at around 8.88°2
. In particular, the peak representing a lattice d-spacing of 14.2Å, interpreted to be an oriented 001 chlorite peak, varies between 14.40 and 14.04Å. Similarly the muscovite 002, talc 002, and kaolinite 001 peaks, represented by high intensities at around 8.88°2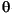 , 9.46°2
, 9.46°2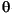 , and 12.46°2
, and 12.46°2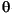 , respectively, are all interpreted to result from mixed layer structures. The net effect of variable phyllosilicate composition on the SIROQUANT analysis is to increase the
, respectively, are all interpreted to result from mixed layer structures. The net effect of variable phyllosilicate composition on the SIROQUANT analysis is to increase the 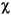 2 value to above 3.00. Nevertheless, the mineral percentages generated by SIROQUANT are believed able to indicate meaningful downhole variation for quartz and carbonate material (see below).
2 value to above 3.00. Nevertheless, the mineral percentages generated by SIROQUANT are believed able to indicate meaningful downhole variation for quartz and carbonate material (see below).
To check the XRD quantification performed by SIROQUANT, 20 samples were analyzed for weight percent carbon. Organic and inorganic carbon content of the uppermost 20 samples in Hole 976B was determined using a UIC Coulometer housed at the Department of Chemical Engineering, University of Sydney. Chemical data are plotted vs. XRD-determined proportions of calcite + dolomite (Fig. 5) and show a clear linear relationship, with the XRD-determined values being mostly <10% higher than the chemically determined values over the range of carbonate values from 20%-40%. The exceptions are samples 161-976B-1H-2, 64-68 cm (XRD determined carbonate is 17.8% higher than the chemically analyzed sample), and 161-976B-8H-5, 77-80 cm (XRD determined carbonate is 2.16% lower than the chemically analyzed sample). Although SIROQUANT was not able to determine accurate values for the carbonate, of more importance to the aims of this study is its ability to reproduce the downhole trend in the carbonate data (Fig. 6). Unfortunately, accurate quantification of the portion of any crystalline phase during SIROQUANT analysis was not possible. Values reported in this study define downhole trends, and subsequent interpretation of data is based on this.
The >63-µm and <20-µm grain-size splits of four selected samples (161-976B-5H-5, 77-82 cm, 161-976B-10H-3, 76-81 cm, 161-976B-15X-3, 76-80 cm, and 161-976B-20X-3, 95-100 cm) were examined using a Jeol JSM 6300F scanning electron microscope (SEM), so that the shape and rounding of the quartz and feldspar grains could be determined. Of particular interest was the texture of these minerals in the <20-µm grain-size fraction, as this was important to interpret whether their origin was detrital or authigenic. The SEM was fitted with a Moran Scientific EDS/XRM analyzer that was employed to confirm mineral identification.
Sedimentation rates based on decompacted sediment thickness were calculated for each pair of sample locations in each hole. Decompacted thicknesses were used in preference to the raw shipboard determinations to enable direct cross-hole correlation of data.
Numeric ages for the calculations were determined from the composite calcareous nannofossil and planktonic foraminiferal biostratigraphic charts given in the preliminary summary of drilling results (Shipboard Scientific Party, 1996b, table 4, for Hole 976B; Shipboard Scientific Party, 1996c, table 5, for Hole 977A; Shipboard Scientific Party, 1996d, table 3, for Hole 978A; and Shipboard Scientific Party, 1996e, table 4 for Hole 979A). Numeric ages for each sample point were calculated by linear interpolation between the mbsf depth/age tie points and are given in Table
2.
Decompacted sediment thicknesses were calculated for each of the mbsf depth/age tie points first using the following relationship determined by Falvey and Middleton (1981):
-
1/
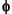 = 1/
= 1/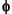 0 + ky, (1)
0 + ky, (1)
(where 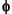 = porosity at any given depth,
= porosity at any given depth, 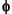 0 = porosity at 0 depth, y = depth, and k = constant related to lithology), to determine a value for k. For this study k = 0.00154605, which was calculated using the porosity data reported by Comas, Zahn, Klaus, et al. (1996) for Hole 976B (Fig. 7) and
0 = porosity at 0 depth, y = depth, and k = constant related to lithology), to determine a value for k. For this study k = 0.00154605, which was calculated using the porosity data reported by Comas, Zahn, Klaus, et al. (1996) for Hole 976B (Fig. 7) and 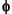 0 = 0.637. Data for Holes 977A and 979A yield almost identical results.
0 = 0.637. Data for Holes 977A and 979A yield almost identical results.
Once determined, k and 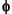 0 were substituted into the following equation from Allen and Allen (1990, p.270):
0 were substituted into the following equation from Allen and Allen (1990, p.270):
-
-
(2)
-
(where y´2 - y´1 = decompacted sediment thickness from any time to the present, and y2 - y1 = sediment thickness given depths y2 and y1), which is solved by iteration.
Decompacted sedimentation rates were calculated between each pair of mbsf depth/age tie points and then linearly interpolated for sample points between these. The resulting values are recorded against the lower of each two points used for the calculation in Table
2. Decompacted sedimentation rates so determined range from less than 50 m/m.y. (419 mbsf, Hole 977A; 2 mbsf, Hole 979A) to in excess of 1000 m/m.y. (470-490 mbsf, Hole 979A).

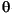 -
-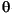 configuration and housed at the Microstructural Analysis Unit at the University of Technology, Sydney. The X-ray source was a long-fine focus copper anode tube emitting X-rays at 1.540562 Å for k
configuration and housed at the Microstructural Analysis Unit at the University of Technology, Sydney. The X-ray source was a long-fine focus copper anode tube emitting X-rays at 1.540562 Å for k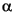 1 and 1.544390 Å for k
1 and 1.544390 Å for k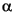 2. Data measurements were made from 2°2
2. Data measurements were made from 2°2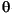 to 70°2
to 70°2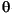 at increments of 0.02°2
at increments of 0.02°2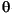 . XRD data were collected for each unsorted sample and for each of the four split fractions. Because of the small sample volume in each grade fraction, all samples were dry sedimented onto 25 x 37.5 mm glass slides, dispersed in distilled water, and dried at 60°C. The >63-µm fractions were ground using a mortar and pestle, before being placed on the glass slides.
. XRD data were collected for each unsorted sample and for each of the four split fractions. Because of the small sample volume in each grade fraction, all samples were dry sedimented onto 25 x 37.5 mm glass slides, dispersed in distilled water, and dried at 60°C. The >63-µm fractions were ground using a mortar and pestle, before being placed on the glass slides.
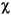 2 value to above 3.00. Nevertheless, the mineral percentages generated by SIROQUANT are believed able to indicate meaningful downhole variation for quartz and carbonate material (see below).
2 value to above 3.00. Nevertheless, the mineral percentages generated by SIROQUANT are believed able to indicate meaningful downhole variation for quartz and carbonate material (see below).
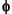 = 1/
= 1/