METHODS

Pore-water data from the Blake Ridge (Fig. 1) were gathered from sediments collected by both ODP operations on Leg 164 and piston coring.

Sediment Sampling and Geochemical Measurements

Procedures for collecting and processing piston core sediments and their pore waters are described in Borowski (1998). Sediments collected from ODP cores were sampled and processed using standard ODP methods, except that pore-water samples were taken more frequently at every ~1.5 m (1 sample per section, or 6 samples per core) (e.g., Fig. 3). Pore waters were extracted from sediments using a hydraulic sediment press (Manheim, 1966) and collected in airtight syringes (Manheim and Sayles, 1974). Sulfate concentration was determined by ion chromatography, and alkalinity was measured by titration (Gieskes et al., 1991). Total carbon dioxide (CO₂) was separated and measured onshore using cyrogenic and manometric techniques (Craig, 1953) from pore-water aliquots stored immediately after squeezing in flame-sealed, airtight ampoules. Methane concentrations within piston core and Site 994 sediments were measured on shipboard using headspace methods (Martens and Klump, 1980; Kvenvolden and McDonald, 1985; Borowski et al., 1997) and normalized to pore space volume (Paull, Matsumoto, Wallace, et al., 1996). Methane concentrations from Site 995 pore waters were measured from subcores transported to an onshore laboratory, and normalized to pore space volume (Hoehler et al., Chap. 8, this volume).

CO₂ was separated and purified using cryogenic techniques (e.g., Craig, 1953). Carbon-isotopic-composition measurements of CO₂ are reported relative to the Peedee belemnite (PDB) standard, and were made using a Delta E mass spectrometer at North Carolina State University (NCSU). The cumulative (vacuum line and mass spectrometer) accuracy and precision of isotopic measurements are ±0.2 and ±0.06 (Neal Blair, pers. comm., 1996).

Sulfur isotopic measurements of interstitial sulfate were made at Geochron Laboratories (Cambridge, MA). Sulfate within pore waters was precipitated as barium sulfate, thermally decomposed to SO₃, and reduced to SO₂ gas for isotopic measurement (Holt and Engelkemeir, 1970). Measurements were made using a VG Micromass mass spectrometer (Model 903), and are reported relative to the Canyon Diablo Troilite (CDT) standard. Measurement precision is ±0.1 and cumulative accuracy is ±0.3 (Marshall Otter, pers. comm., 1997).

Diagenetic Model

Variations in the concentration of interstitial constituents relative to time and depth can be described by equations relating the mass-transport processes of diffusion, advection (burial and compaction) to consumption and production reactions (e.g., Berner, 1980). The general diagenetic equation used here is

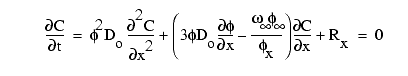  (3)

where C is concentration, t is time, is porosity, D_o is the free-solution diffusion coefficient, x is depth below the sediment-water interface, is sedimentation or burial rate, and R is reaction rate (Berner, 1964, 1977). The subscript () refers to the depth where /x approaches zero. This form of the diagenetic equation was initially applied to anoxic, methane-oxidizing sediments by Murray et al. (1978).

The model explicitly assumes that: (1) steady state conditions occur (i.e., C/t = 0); (2) vertical concentration gradients are much greater in magnitude than horizontal gradients; (3) sediment burial, compaction, and molecular diffusion are the only mass-transport processes (no fluid advection, bioirrigation, or gas ebullition occurs); (4) the free-solution diffusion coefficient and sediment density are constant with depth; and (5) the diffusion coefficient within sediment (D_s) is related to free-solution diffusion coefficient by the expression, D_s = ² D_o (Ullman and Aller, 1982).

An inverse, numerical model was used to predict reaction rates and their depth distribution using Equation 3 by solving for R_x for data collected at Site 995 (for model parameters see Table 1). Cubic spline functions were used to fit methane concentration data providing the necessary gradient information used to calculate the first and second derivative terms of Equation 3. Cubic splines are particularly good for fitting purposes because they: (1) have no inherent functional form (e.g., like exponential or polynomial functions); (2) have continuous first and second derivatives; and (3) can be modified to accept measurement uncertainties (Ahlberg et al., 1967; Alperin, 1988; Alperin et al., 1988). Porosity data (Paull, Matsumoto, Wallace, et al., 1996) were fit using an exponential function that provided _x and . The free-solution coefficient (D_o) used for methane was 7.9 10^-6 cm² s^-1 (3ºC; calculated from empirical data given by Li and Gregory, 1974; Lerman, 1979), based on a sediment temperature of ~4ºC (Ruppel, 1997). The sedimentation rate was assumed to be constant at 0.0057 cm y^-1 (5.7 cm ky^-1), based on the last appearance of Pseudoemiliania lacunosa (Paull, Matsumoto, Wallace, et al., 1996), which occurred at 0.46 Ma (Thierstein et al., 1977).