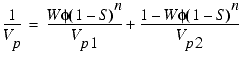,
(1)
This section reviews the essentials of the theory necessary for the computation of the amount of hydrate concentrated in the sediment's pore space. The relation between the velocity and hydrate concentration in the pore can be described by the following three-phase weighted equation. This equation predicts the velocity for the unconsolidated sediment with high porosity such as the sediment in the study area. The weighted equation is defined as a weighted combination of the time-average equation (Timur, 1968), which predicts velocity in a rigid, consolidated rock with little fluid, and the Wood equation (Wood, 1941), which pertains to particles in suspension.
A three-phase weighed equation is defined as (Lee et al., 1996):
,
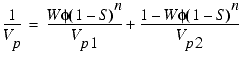(1)
where Vp
= compressional (P) velocity of hydrated sediments; Vp1
= compressional velocity of hydrated sediments computed from the three-phase
Wood equation; Vp2 = compressional
velocity of hydrated sediments computed from the three-phase time-average
equation; W = a weighting factor; 
= sediment porosity (as a fraction); S = concentration of hydrate in
the pore space (as a fraction); and n = a constant simulating the rate
of lithification with hydrate concentration.
The three-phase Wood equation (Wood, 1941) is given by
,
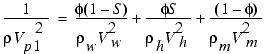(2)
where 
w
is the density of the fluid, h
is the density of pure hydrate, m
is the density of matrix, and
is the bulk density of sediments. The bulk density is given by
.
(3)
The three-phase time average equation (Pearson et al., 1983; Timur, 1968) can be written as
,
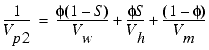(4)
where Vw is the compressional velocity of the fluid, Vh is the compressional velocity of pure hydrate, and Vm is the compressional velocity of the matrix. In this formulation, Vm is a modified matrix velocity as defined in Lee et al. (1996), which is the "grain" or "matrix" velocity computed at zero porosity considering the effect of clay content (Castagna et al., 1985).
As indicated in Equation 1, when the concentration of hydrate equals zero (S = 0), Equation 1 is identical to the Nobes et al. (1986) equation, irrespective of exponent n. A value W > 1 favors the Wood equation and W < 1 favors the time-average equation. As n increases, the weighted equation approaches the time-average equation more rapidly, because (1 - S) is less than or equal to 1. The weighting factor (W) can be estimated using the velocity vs. porosity data for sediments with no hydrate concentration (Lee et al., 1996).
