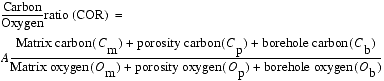.(1)
The GLT (Fig. 1) consists of four parts: a natural gamma-ray spectrometry sensor (NGT); a neutron porosity tool (CNT-G), which carries a 252Cf source of neutrons (2 MeV source instead of the conventional 4.5 MeV AmBe source) that is used in conjunction with the aluminum activation clay tool (AACT) (Hertzog et al., 1989); and the gamma-ray spectroscopy tool (GST). The NGT measures natural gamma-ray emissions that are used to quantify the potassium, thorium, and uranium content of the logged sediments. The lower energy of the californium source in the CNT-G, compared to the standard AmBe source, reduces the number of fast neutron reactions that would interfere with the AACT measurement. Neutron (emitted by the 252Cf source) capture by 27Al results in the formation of 28Al, which decays to 28Si with a half-life of 1.3 min and emits gamma rays with an energy spectrum of 1.78 MeV, which is measured by the AACT (Scott and Smith, 1973). The AACT is similar to the NGT, but the AACT measures the gamma-ray spectrum of the activated formation in three additional windows. Comparing AACT measurements with those from the NGT results in a measure of the concentration of Al (wt%). The GST is located at the base of the tool string (Fig. 1) and consists of a high-energy pulsed neutron accelerator (14 MeV) and a NaI scintillation crystal detector. In neutron spectroscopy downhole logging, each element has a characteristic gamma ray that is emitted from a given neutron-element interaction. An element, therefore, can be identified by its gamma-ray spectrum, with the intensity of emission related to the atomic elemental concentration. By combining elemental yields from neutron spectroscopy logs, reservoir parameters including porosities, lithologies, formation-fluid salinities, and hydrocarbon saturations (including gas hydrate) can be calculated. The GST can be operated in two timing modes: inelastic, which mainly measures the neutron reactions in the high energy range (elements quantified: carbon, calcium, iron, oxygen, sulfur, silicon), and capture-tau mode, which measures the gamma rays emitted from neutron capture (elements quantified: calcium, chlorine, iron, hydrogen, sulfur, and silicon). In ODP boreholes, the GST is usually operated in only capture-tau mode; however, on Leg 164 a selected number of inelastic measurements were made (discussed in more detail later in this report). Calculation of absolute concentrations (wt%) of elemental oxides require additional post-field processing to estimate the contribution of rare-earth elements (gadolinium and samarium in particular) and titanium. See Shipboard Scientific Party (1996a) for additional information on required downhole log data processing.
As previously indicated, the GST measures the amount of carbon, calcium, iron, oxygen, sulfur, silicon, chlorine, and hydrogen within a rock sequence. The amount of a particular element in a rock is not only controlled by the matrix mineralogy, but also by the amount of water and hydrocarbons, including gas hydrate, that are stored in a porous rock unit. The elemental ratio that shows promise of yielding gas hydrate-reservoir saturations is the carbon/oxygen gamma-ray ratio. Using molecular stoichiometry, it is possible to calculate the amount of carbon and oxygen that are present in a cubic centimeter of pore volume or (sediment) matrix for the following substances: water, methane gas, ice, structure-I methane hydrate, sandstone (quartz) matrix, limestone (calcite) matrix, clay (smectite, illite, chlorite, and kaolinite) matrix, and dispersed organic carbon (Table 1). The process used to calculate the elemental content of the various reservoir constituents listed in Table 1 is described in Collett (1998). The chemical formula and bulk density of the individual reservoir constituents were used to calculate the number of carbon and oxygen atoms present in one cubic centimeter of each substance. The elemental calculations for the four clays (Table 1: smectite, illite, chlorite, and kaolinite) being considered are complicated because of the highly variable chemical nature of clays. In this example, we have selected standard "end-member" chemical formulas and bulk densities for the four types of clays being modeled.
By using simple mixing rules and the elemental concentrations in Table 1, it is possible to develop elemental relations (ratios) that yield gas hydrate-reservoir saturations. Depicted in Figure 2 and Figure 3 are the results of the carbon/oxygen reservoir modeling. All of the reservoir conditions modeled are derivations of a simple three-component reservoir model that consists of either a quartz or calcite matrix (no clay), gas hydrate, and either water, ice, or methane gas. The carbon/oxygen and porosity (0%-60%) crossplots in Figure 2 and Figure 3 are similar to conventional oil and gas carbon/oxygen "fan charts" (Woodhouse and Kerr, 1992). Of concern, however, is the limited range of expected carbon/oxygen ratios in gas hydrate-bearing sandstone (quartz) reservoirs (Fig. 2). For example, the maximum range of the carbon/oxygen ratio for a gas hydrate- and water-bearing reservoir (Fig. 2A) with 40% porosity would only be 0.04, which is near the likely uncertainty of the carbon/oxygen log measurement (Woodhouse and Kerr, 1992). The uncertainty in carbon/oxygen log measurements in gas hydrate-bearing limestone (calcite) reservoirs should be less of a problem.
The uncertainty in the carbon/oxygen determined gas hydrate saturations are dependent on the uncertainty of each measurement in the interpretation procedure. Woodhouse and Kerr (1992) showed that the maximum precision of the carbon/oxygen ratio measurement can be reduced to about ±0.008. However, when the uncertainties in the other required measurements are considered, such as determining the carbon and oxygen content of the matrix and borehole fluids, the uncertainty in the log-measured carbon/oxygen water saturations may be as great as 47%. To further evaluate the likely uncertainty in the GST-derived carbon/oxygen ratios and water saturations for various reservoir porosities, we used the approach described by Woodhouse and Kerr (1992) in which the uncertainty of each measurement in the carbon/oxygen interpretation "chain" is assessed. Table 2 contains the calculated uncertainty in the GST-derived carbon/oxygen water saturations for a wide range of reservoir porosities. The uncertainty in carbon/oxygen-derived water saturations decreases rapidly as porosity increases. At high porosities, such as in most known gas hydrate occurrences, the quantities of formation-fluid carbon and oxygen are high and the accuracy of the GST-derived gas hydrate saturations could be relatively fair to good. For example, in a gas hydrate- and water-bearing reservoir (porosity of 60%), the uncertainty in the carbon/oxygen-calculated water saturations would be about 7%. Additional downhole calibration of the carbon/oxygen interpreted water saturations in known water-saturated zones (no hydrocarbon) allows the uncertainties in the carbon/oxygen measurements to be reduced further (Woodhouse and Kerr, 1992).
In the previous discussion, we have generated a series of carbon/oxygen "fan charts" for relatively simple reservoir conditions; however, we need to develop a more complete understanding of the chemistry of the entire borehole environment. The amount of carbon or oxygen measured by the GST is not only controlled by the chemistry of the pore-fluids within the formation, but also by the chemistry of borehole fluids and rock matrix. An equation relating all of the carbon and oxygen sources associated with a borehole was developed by Hertzog (1978):
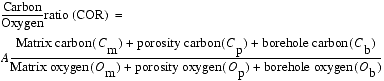.(1)
The coefficient A is determined by the relative inelastic neutron cross section of carbon and oxygen, and it is essentially constant over a variety of conditions. Direct calculations of the coefficient A and Monte Carlo simulations have yielded a value of 0.75 for the coefficient A in a wide range of formations (Roscoe and Grau, 1988). The matrix carbon (Cm) term is the sum of the various matrix volumes and their carbon concentrations. Carbonates, including limestone and dolomite, will normally be the only significant contributors of matrix carbon in conventional reservoirs. However, organic carbon can be relatively abundant in marine sediments. The porosity carbon (Cp) term is essentially due to the presence of hydrocarbons. The matrix oxygen (Om) term is a more comprehensive sum than the matrix carbon (Cm) term, because oxygen is present in most all of the matrix constituents (Table 1). The porosity oxygen (Op) term is mainly the product of the water content of the formation in conventional hydrocarbon reservoirs. The remaining two terms in Equation 1 are the borehole contribution to the carbon (Cb) and oxygen (Ob) yields. Borehole carbon and oxygen content is a function of the borehole size, the outside diameter of the tool and sleeve, and the chemical composition of the borehole fluids. These factors need to be evaluated to account for potential borehole effects on the GST measurements. Equation 1 can be expanded to take into account the carbon and oxygen content of various borehole constituents in conventional hydrocarbon reservoirs:
,
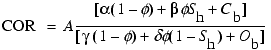(2)
where COR = log measured
carbon-oxygen ratio; A = ratio of average carbon and oxygen fast
neutron cross sections; 
=
porosity, decimal percent; Sh
= hydrocarbon (gas hydrate) saturation, decimal percent; Cb
= relative carbon concentration contribution from the borehole, variable units; Ob
= relative oxygen concentration contribution from the borehole, variable units; 
= atomic concentration of carbon in the matrix, variable units; 
= atomic concentration of carbon in the formation fluid (gas hydrate), variable
units; 
=
atomic concentration of oxygen in the matrix, variable units; and 
= atomic concentration of oxygen in the formation fluid (water), variable units.
In Equation 2, each constituent is weighted according to its bulk volume and the atomic concentration of carbon and oxygen atoms per cubic centimeter that it contains. The variables Cb and Ob account for the borehole background signal, which are typically Ob = 0.05 and Cb = 0.0 in water-filled holes (expressed in units of Avogadro's number) (Woodhouse and Kerr, 1992). The borehole oxygen (Ob) and carbon (Cb) correction variables can also be directly calculated for a given borehole and tool configuration. Roscoe and Grau (1988) demonstrated that the borehole oxygen (Ob) and carbon (Cb) correction variables are calculated by first determining the volume of oxygen and carbon in the borehole. Each portion of the borehole (including casing, cements, and tool sleeves) that contributes to the carbon (Cb) and oxygen (Ob) borehole correction variables needs to be individually assessed. Therefore, Ob and Cb have been parameterized with a volumetric parameter representing the borehole volume of carbon-bearing (Vc) and oxygen-bearing (Vo) material. These variables can be calculated from the relation
where do2 and di2 are the outside and inside diameters of the regions of interest, respectively. The borehole volumetric parameters Vo and Vc are obtained by summing the Vx values from all the regions of interest in the borehole. For example, in a 30-cm open (uncased) water-filled borehole the volume of water (Vo) measured by the GST (3.475-cm-diameter tool) would be 887.9 cm2. The volume of carbon-bearing borehole fluids (Vc) in the same borehole would be zero since the hole is filled with only water (no hydrocarbons). If a sleeved tool is used, however, the Vc of the sleeve needs to be calculated in the same manner as the example Vo calculation and included in the Cb correction variable. Roscoe and Grau (1988) presented a series of comparison graphs that can be used to determine values for Ob and Cb from the calculated Vo and Vc values for various borehole conditions. Roscoe and Grau (1988) also demonstrated, however, that the actual value of Ob and Cb is affected by changes in sediment porosities. This Ob and Cb porosity dependence can be mathematically determined with the following relation:
(
- 0.17)], (4)
where Ob
is the porosity corrected value of Ob'
and is the porosity
correction constant, which has been determined to be 0.61 (Roscoe and Grau,
1988). Because ,
,
,
and
are constants for a specified mineralogy and fluid, and Cb
and Ob
are constants for a particular borehole configuration, hydrocarbon saturations (Sh)
can be calculated directly from the COR if the matrix porosity is known.
Equation 2 yields accurate hydrocarbon saturations in conventional oil and gas
reservoirs, where all of the porosity oxygen term (Op)
is the product of the water content of the formation. In gas hydrate-bearing
sediments, however, the occurrence of oxygen in the water molecules associated
with the gas hydrate structure will also contribute to the porosity oxygen (Op)
term. The effect of gas hydrate-associated oxygen content on the GST measured
carbon/oxygen ratios can be explicitly explained by adding a gas hydrate oxygen
term to Equation 2:
,
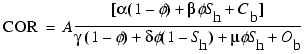(5)
where µ is the atomic
concentration of oxygen atoms in a Structure-I methane hydrate. The matrix
mineralogy data necessary to assign values for the parameters
and
may be obtained from the GLT-derived elemental lithologic indicator ratios or
LIR (ratio of Si/Ca), which is used to assess relative amounts of quartz and
calcite in the matrix. For mixed quartz and calcite formations
= 0.027(1 - LIR) and =
0.081 + 0.007 LIR (expressed in units of Avogadro's number) (Woodhouse
and Kerr, 1992). The COR hydrocarbon saturation equation (Eq. 5) can be modified
to accommodate more complex mixtures of minerals, provided their atomic
concentration coefficients are known. Accurate interpretation of COR data
requires precise chemical analysis of all potential reservoir constituents (Table
1).
It is generally accepted that inelastic-scattering measurements of carbon and oxygen concentrations are largely insensitive to dissolved salts in the pore waters or shaliness (clay content) of the formation (Woodhouse and Kerr, 1992). However, little work has been conducted to evaluate the effect of clay-rich marine sediments on carbon/oxygen ratios. In some holes, the clay content of the formation sediments exceeds 60%. When considering the effect of clays on carbon/oxygen-calculated gas hydrate saturations, we will assume that clays contain no carbon. Carbon, however, is often concentrated in organic-rich marine sediments that will be dealt with later in this report. In general, the oxygen content of quartz and most clay minerals are similar (Table 1). Therefore, in conventional quartz matrix reservoirs the effect of small amounts of clay (5%-10% of matrix) on the GST-derived carbon/oxygen ratios are negligible. However, in clay-rich marine sediments the small difference in the oxygen content between most clays and quartz may have a significant effect on the carbon/oxygen ratio of the sediment matrix. In Figure 4, we have crossplotted with porosity (ranging from 0% to 40%) the expected carbon/oxygen ratio in a quartz and three pure-clay (kaolinite, illite-chlorite, and montmorillonite) matrix reservoirs with various gas hydrate saturations (Sh of 0%, 25%, 50%, 75%, and 100%). The pure illite and chlorite matrix reservoirs are shown as a single clay type in Figure 4 because illite and chlorite contain the same amount of oxygen per unit volume. At relatively high gas hydrate saturations and high reservoir porosities, the effect of clays on the GLT-derived carbon/oxygen ratios are the greatest. As shown in Figure 4, a 100% gas hydrate-saturated pure montmorillonite "reservoir" with 40% porosity would be characterized with a carbon/oxygen ratio of 0.045, which is about 0.005 higher than the carbon/oxygen ratio for a pure quartz matrix reservoir under the same conditions. A 0.005 carbon/oxygen difference, however, is below the resolution capability of the GST (discussed earlier in this report). Figure 4 confirms that the occurrence of clay in most conventional reservoirs (porosity <30%, clay content <10%) and marine sediments have little to no effect on inelastic-neutron carbon/oxygen measurements.
Organic carbon can be
concentrated in fine-grained marine sediments. For example, on the Blake Ridge
the total organic carbon content (TOC) of the sediment ranges from 0.5 to 2.0
wt% (Shipboard Scientific Party, 1996b, 1996c, 1996d). The GST will detect and
measure the volume of organic carbon in marine sediments, which could have a
significant effect on carbon/oxygen-calculated hydrocarbon saturations. To
evaluate the potential effect of dispersed sedimentary organic carbon on neutron
spectroscopy measurements we need to calculate the atomic concentration of
carbon atoms within a given volume of organic carbon as it would occur in
nature. We have calculated that there is about 6.0 
1022 carbon atoms within a cubic centimeter of pure organic carbon (Table
1), assuming a grain density of 1.2 g/cm3 (Serra, 1984). In Figure
5 and Figure 6, we have
crossplotted with porosity (ranging from 0% to 60%) the expected carbon/oxygen
ratio in pure quartz (Fig. 5)
and calcite (Fig. 6) matrix
reservoirs that are 100% saturated with either water or gas hydrate. Also shown
in Figure 5 and Figure
6 are plots of the same reservoir conditions, except 2% of the quartz
and calcite matrix are replaced with organic carbon. As shown in Figure
5 and Figure 6, the
addition of organic carbon to the sediment matrix will significantly affect
measured carbon/oxygen ratios. The addition of 2% organic carbon to a pure block
of quartz or calcite (no porosity) results in a 0.023 and 0.025 increase in the
carbon/oxygen ratio, respectively. The effect of organic carbon content on the
GST-measured carbon/oxygen ratios can be explicitly explained by the following
four-component COR equation, which is a modified version of the standard
three-component equation (Eq. 2):
,
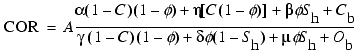(6)
where C is the
organic carbon content of the sediment as a volume fraction and 
is the atomic concentration (variable units) of carbon atoms in natural
occurring organic carbon. This four-component equation can be used to
characterize a water- and gas hydrate-bearing reservoir with a matrix consisting
of a mixture of quartz, calcite, and organic carbon.
