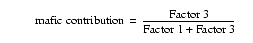 .
.
The concentrations of Zr, Nb, Ba, Y, Cr, V, Ni, Cu, Zn, Mn, Rb, and Ti show large variations downhole (Fig. 4, Fig. 5) that are sensitive to the presence or absence of sand. There is also variability in the mud-dominated intervals in the hole, however, indicating a second control that may be related to changes in the provenance of the fine-grained fraction. To distinguish semiquantitatively the common causes (factors) for variations in the distributions of these 12 "detrital" elements, such as the changes in grain-size and provenance, we have conducted Q-mode factor analysis using the element concentration data.
Prior to the factor analysis, the total concentrations of the 12 elements were normalized to unity as follows:
This normalization eliminates apparent fluctuations in concentration attributable to dilution by biogenic materials. It also permits us to convert the factor scores and loadings, respectively, into the original elemental compositions and the actual contribution of each factor to discrete samples (Miesch, 1976). Following the normalization, each variable (as the normalized content of each element) was then proportionally rescaled to set the maximum and minimum values to one and zero, respectively. Q-mode factor analysis with varimax rotation was performed on these rescaled data (Miesch, 1976).
The Q-mode analysis yields three factors that explain 97% of the total variance in the rescaled data, implying three common end-members within the sediments. The extracted varimax factors are denoted Factor 1 through 3 in descending order of the variance explained by each. The compositions of each end-member were calculated from its varimax factor scores (Miesch, 1976) and are shown in Table 2 as element:Ti ratios. Two types of relationships between the selected element ratios in end-members and those in the samples are also shown in Figure 6. Temporal variations in the contributions of the three end-members calculated from their factor loadings are shown in Figure 7A, 7B, where the total sum of Factors 1 to 3 is unity.
Factor 2 is characterized by higher Zr/Ti, Nb/Ti, Y/Ti, Ba/Ti, and Cr/Ti ratios (Table 2; Fig. 6). The contribution of Factor 2 is highest in samples from sandy layers or lenses (Fig. 7A). Figure 7A also shows the volume percentage (vol%) of the silt-sized component within the detrital fraction of nonsand samples. These were selected mostly from the upper 2 m of the hole to examine grain-size changes within the mud-dominated intervals (Tada et al., Chap. 25, this volume). They show that the contribution of Factor 2 varies to some degree in harmony with the silt content (as vol%) even in the mud-dominated intervals. Thus, Factor 2 is interpreted as representing the coarser (sand and silt) portion of the detrital fraction.
The contributions of Factors 1 and 3 are lowest in samples from sandy layers or lenses (Fig. 7B). Thus, these two factors are expected to reflect the compositions of the fine fractions of terrigenous detritus from different sources. Factor 3 is distinguished from Factor 1 by its higher V/Ti, Ni/Ti, and Mn/Ti, and lower Rb/Ti, Cu/Ti, Zn/Ti, and Ba/Ti ratios (Table 2; Fig. 6). Relative enrichments of compatible elements such as V and Ni and depletion of incompatible elements such as Rb and Ba within Factor 3 imply that this factor represents contributions to the deposits from a mafic source or sources (Wilson, 1989). To examine temporal variations in relative contributions from different source rocks (essentially mafic vs. felsic) within the fine detrital fraction, the mafic contribution is defined as
The results are shown in Figure 7C. Although not perfect, this approach filters out much apparent variation that could result from dilution by the coarser fraction.