LABORATORY METHODS
Samples for sand petrography were immersed in 3% H2O2 solution for at least 24 hr to remove organic material. Sodium hexametaphosphate solution (4 g/1000 mL) was added to disaggregate and disperse clays. Suspensions were placed on a magnetic stirrer, then wet sieved with a 63-Ám screen. The fine fractions were saved for X-ray diffraction analysis. After drying the coarse fraction, standard thin sections were prepared from epoxy grain mounts, and plagioclase and potassium feldspars were stained following Houghton (1980). We used the Gazzi-Dickinson point-counting method, whereby all sand-sized minerals are assigned to their respective mineral categories, even if they occur in polycrystalline rock fragments (Dickinson, 1970). A sand-sized plagioclase phenocryst in a volcanic-rock fragment, for example, counts as plagioclase rather than the host lithic grain. Ingersoll et al. (1984) demonstrated that this approach significantly reduces the sensitivity of compositional data to grain size. Step sizes for point counts were 0.4 mm between tracks and 0.6 mm along tracks. At least 500 grains were counted per thin section. Grain types were assigned to 22 categories, then combined into conventional monocrystalline and polycrystalline modes
(Table 1). Replicate analyses showed that the average standard deviations for these detrital modes (in percent) are: Q = 4, F = 4, and L = 3; Qm = 3, F = 4, and Lt = 3; Qm = 5, P = 5; and K = 2; and Qp = 5, Lv = 6, and Lsm = 5 (Saettler, 1998).
Samples of turbidite matrix and hemipelagic mud were prepared for X-ray diffraction analysis using the same techniques. After sieving, all <63-Ám suspensions were disaggregated further using an ultrasonic cell probe, then centrifuged at 1000 rpm for 2.4 min to separate the <2-Ám fraction. Oriented aggregates of the <2-Ám fraction were collected on vacuum filters, peeled onto glass slides, and saturated with ethylene glycol vapor for at least 12 hr at 60°C before scanning. We used a Scintag Pad V X-ray diffractometer, with CuK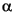 radiation (1.54 ┼) and a Ni filter. Scans were run at 40 kV and 30 Ma from 3 to 19°2
radiation (1.54 ┼) and a Ni filter. Scans were run at 40 kV and 30 Ma from 3 to 19°2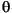 at a rate of 2°2
at a rate of 2°2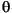 /min and a step size of 0.01°2
/min and a step size of 0.01°2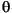 . Processing of digital data utilized MacDiff software to smooth counts, determine background levels, and calculate peak intensities and peak areas. To help facilitate comparisons with existing data from the region (e.g., Karlin, 1980), the integrated areas of smectite (001), illite (001), and chlorite (002) peaks were multiplied by Biscaye (1965) weighting factors (1x, 4x, and 2x, respectively), then normalized to 100%. Chlorite content was calculated using the peak near 12.5°2
. Processing of digital data utilized MacDiff software to smooth counts, determine background levels, and calculate peak intensities and peak areas. To help facilitate comparisons with existing data from the region (e.g., Karlin, 1980), the integrated areas of smectite (001), illite (001), and chlorite (002) peaks were multiplied by Biscaye (1965) weighting factors (1x, 4x, and 2x, respectively), then normalized to 100%. Chlorite content was calculated using the peak near 12.5°2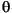 (d-value = 7.10 ┼), but peak interference can be problematic if there is a strong kaolinite (001) reflection (d-value = 7.16 ┼). Consequently, nine samples were tested for kaolinite content by boiling in 1-N HCl for 2 hr (Biscaye, 1964). The kaolinite contribution proved to be less than 7% of the composite peak area, with an average of 5% (Saettler, 1998). Three types of error in the precision of mineral percentages were tested by replicate analysis: natural inhomogeneity of subsamples (<4%), diffractometer instability (<2%), and inconsistent manipulation of data-processing software (<1%). Accuracy of the Biscaye (1965) weighting factors, however, also varies with the absolute abundance of each mineral (e.g., Underwood et al., 1993). Moore and Reynolds (1997) concluded that accuracy is generally no better than 10% for major constituents. Our data, therefore, should be regarded as semiquantitative estimates and used to compare relative trends in mineralogy rather than as absolute abundance.
(d-value = 7.10 ┼), but peak interference can be problematic if there is a strong kaolinite (001) reflection (d-value = 7.16 ┼). Consequently, nine samples were tested for kaolinite content by boiling in 1-N HCl for 2 hr (Biscaye, 1964). The kaolinite contribution proved to be less than 7% of the composite peak area, with an average of 5% (Saettler, 1998). Three types of error in the precision of mineral percentages were tested by replicate analysis: natural inhomogeneity of subsamples (<4%), diffractometer instability (<2%), and inconsistent manipulation of data-processing software (<1%). Accuracy of the Biscaye (1965) weighting factors, however, also varies with the absolute abundance of each mineral (e.g., Underwood et al., 1993). Moore and Reynolds (1997) concluded that accuracy is generally no better than 10% for major constituents. Our data, therefore, should be regarded as semiquantitative estimates and used to compare relative trends in mineralogy rather than as absolute abundance.

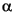 radiation (1.54 ┼) and a Ni filter. Scans were run at 40 kV and 30 Ma from 3 to 19°2
radiation (1.54 ┼) and a Ni filter. Scans were run at 40 kV and 30 Ma from 3 to 19°2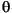 at a rate of 2°2
at a rate of 2°2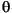 /min and a step size of 0.01°2
/min and a step size of 0.01°2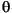 . Processing of digital data utilized MacDiff software to smooth counts, determine background levels, and calculate peak intensities and peak areas. To help facilitate comparisons with existing data from the region (e.g., Karlin, 1980), the integrated areas of smectite (001), illite (001), and chlorite (002) peaks were multiplied by Biscaye (1965) weighting factors (1x, 4x, and 2x, respectively), then normalized to 100%. Chlorite content was calculated using the peak near 12.5°2
. Processing of digital data utilized MacDiff software to smooth counts, determine background levels, and calculate peak intensities and peak areas. To help facilitate comparisons with existing data from the region (e.g., Karlin, 1980), the integrated areas of smectite (001), illite (001), and chlorite (002) peaks were multiplied by Biscaye (1965) weighting factors (1x, 4x, and 2x, respectively), then normalized to 100%. Chlorite content was calculated using the peak near 12.5°2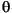 (d-value = 7.10 ┼), but peak interference can be problematic if there is a strong kaolinite (001) reflection (d-value = 7.16 ┼). Consequently, nine samples were tested for kaolinite content by boiling in 1-N HCl for 2 hr (Biscaye, 1964). The kaolinite contribution proved to be less than 7% of the composite peak area, with an average of 5% (Saettler, 1998). Three types of error in the precision of mineral percentages were tested by replicate analysis: natural inhomogeneity of subsamples (<4%), diffractometer instability (<2%), and inconsistent manipulation of data-processing software (<1%). Accuracy of the Biscaye (1965) weighting factors, however, also varies with the absolute abundance of each mineral (e.g., Underwood et al., 1993). Moore and Reynolds (1997) concluded that accuracy is generally no better than 10% for major constituents. Our data, therefore, should be regarded as semiquantitative estimates and used to compare relative trends in mineralogy rather than as absolute abundance.
(d-value = 7.10 ┼), but peak interference can be problematic if there is a strong kaolinite (001) reflection (d-value = 7.16 ┼). Consequently, nine samples were tested for kaolinite content by boiling in 1-N HCl for 2 hr (Biscaye, 1964). The kaolinite contribution proved to be less than 7% of the composite peak area, with an average of 5% (Saettler, 1998). Three types of error in the precision of mineral percentages were tested by replicate analysis: natural inhomogeneity of subsamples (<4%), diffractometer instability (<2%), and inconsistent manipulation of data-processing software (<1%). Accuracy of the Biscaye (1965) weighting factors, however, also varies with the absolute abundance of each mineral (e.g., Underwood et al., 1993). Moore and Reynolds (1997) concluded that accuracy is generally no better than 10% for major constituents. Our data, therefore, should be regarded as semiquantitative estimates and used to compare relative trends in mineralogy rather than as absolute abundance.