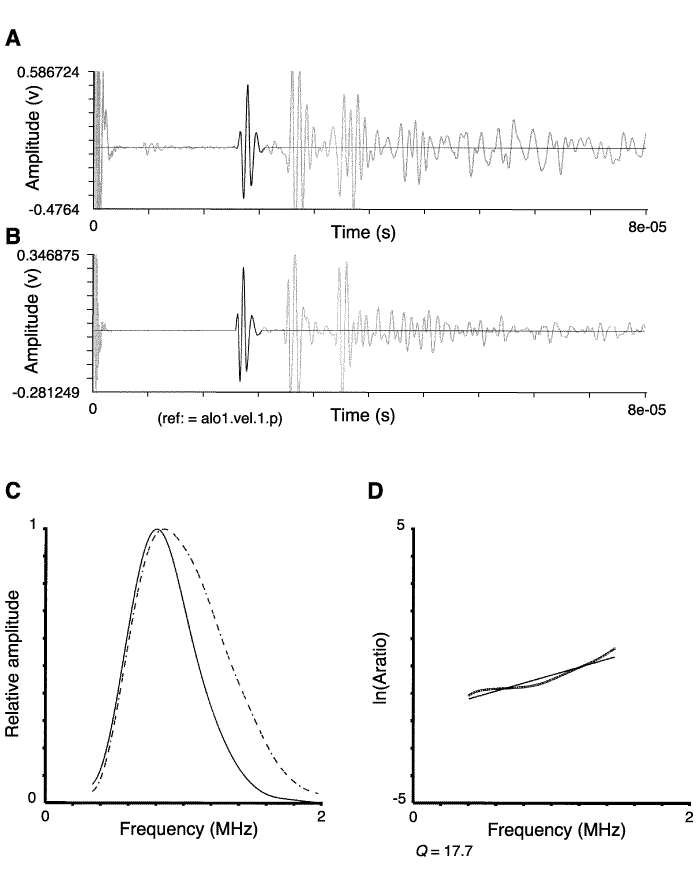
Figure F4. The spectral ratio method is applied to obtain compressional wave attenuation by comparing the spectra from an aluminum reference to the spectra for a gabbro sample. A. Time series of the pulse through gabbro. The spectra is computed for the waveform with a bold line. B. The pulse through the aluminum reference is unattenuated. C. The spectra are compared: solid line = gabbro, dashed line = aluminum. The loss of high frequencies due to attenuation in the gabbro is evident. D. The natural logarithm of the ratio of the two spectra is displayed as a function of frequency as open circles. The solid line through these open circles is the least-squares fit line. For intrinsic attenuation in an infinite, homogeneous medium, theory predicts that the natural logarithm of spectral ratios should be a straight line. Q is computed from the slope (m) of the ratio of the spectral values of the aluminum to the gabbro as follows: Q = 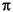x_gab/(c x m), where x_gab = the propagation distance in gabbro, and c = the compressional velocity in gabbro. In this case, Q = 17.7.