-
F = D
C/x, and
C/t = D2/x2,
The elementary processes of mass transport in geomaterial are not only advection but also diffusion. Diffusion describes the mass transfer process due to the random thermal motion of molecules, ions, and atoms (also known as Brownian motion), which is represented by a molecular random walk. Diffusion causes mass flux down a concentration gradient and results in the spreading of a concentration front with time toward the random distribution of molecules for increasing entropy. The mass flux per unit cross-sectional area depends on the concentration gradient, known as Fick's first and second laws (Fick, 1855) and is expressed as follows:
C/x, and
C/t = D2/x2,
where D is the diffusion coefficient and C/x is the concentration gradient.
Trough diffusion experiments were used for the measurement of effective diffusion coefficients (Fig. F4A). Rock samples were fitted tightly into the central support member of the cell, and the space between the rock disk and the acrylic central support member was sealed with a silicone gasket. There are two cells on both sides of the sample, one for a tracer and another for pure water. Samples were soaked in pure water under vacuum for 1 week to evacuate all air from the interconnected pores. The experiments were conducted under the following conditions: 25°C temperature and atmospheric pressure. Potassium iodine solution (concentration = 1 mol/L) was used as a tracer because the iodine ion is generally not adsorbed on the surface of the rock matrix.
The solution of Fick's second law (Crank, 1975) under an initial condition of
for
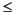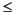x 1
and boundary conditions of
is expressed as:
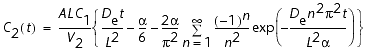
where
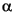= rock capacity factor.
The above diffusion equation approaches for a sufficient long time, t, the following expression for the concentration in the pure water vessel:
At this time, this diffusion process can be treated as a steady state and the effective diffusion coefficient can be calculated by the line slope of ion concentration with time (Fig. F4B). Iodine and potassium ions were measured by an ion-selective electrode and atomic absorption spectrometry, respectively.
The concentrations of iodine and potassium ions during the diffusion experiments are plotted as a function of time (Figs. F5, F6). All the plots indicate that the concentrations increase with time, showing a transient part and a steady-state slope. As mentioned above, the effective diffusion coefficient is calculated by the linear slope of the data. The effective diffusion coefficient can be calculated using the slope, geometry, and volume of the cell (Table T1).
