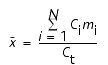
Because the whole-round samples for geotechnical tests were taken from hemipelagic sediments and the muddy intervals of the turbidite-rich facies, the grain-size samples are exclusively fine grained. Samples were freeze-dried and weighed. They were then placed in a beaker and treated with 3% H2O2 for a minimum of 24 hr until digestion of organic matter had ceased. Samples were then dispersed with 250 mL of 4 g/L sodium hexametaphosphate (Calgon) for a minimum of 24 hr and further dispersed via 10 min of exposure in an ultrasonic bath. Highly indurated mudstones were exposed to gentle crushing and longer treatment periods with frequent stirring.
We separated the <63-Ám fraction by wet sieving. Fluid volume of the silt and clay suspension was then brought to 500 mL with deionized, distilled water and vigorously agitated. For 45 of the samples, a 20-mL aliquot was extracted from a depth of 20 cm. We corrected for the presence of Calgon in each aliquot by subtracting 0.04 g, and the result was multiplied by 25 in order to obtain a weight for the fine-grained fraction without organic matter.
We then reagitated and removed a few milliliters of sediment suspension with a disposable pipette. This suspension was further diluted in deionized water, and a few drops of the diluted suspension were placed in a clear glass bottle of filtered deionized water, taking care to ensure thorough mixing of the suspension throughout the process. This dilute suspension was scanned with the laser particle counter as described below in order to distinguish between the abundances of clay- and silt-sized particles.
In order to estimate the percent clay vs. percent silt in the <63-Ám fraction, we used a Spectrex PC-2000 laser particle counter (LPC). The LPC measures the cross-sectional dimension of particles by light scattering. A laser diode rotates at a constant rate, illuminating a volume of water in which sediment is suspended. As the beam strikes a particle, the light is scattered, and the scattered light is collected by a photodetector. This causes an electrical pulse in the connected preamplifer, and the amplitude and width of the pulse is a function of the grain size (Spectrex Corporation, 1998). The LPC is rapid; it is possible to measure the grain-size distribution in 30 s.
Typical output from the LPC may be seen in Table T1. The output includes the number of counts per cubic centimeter that fall into each size bin. Sixteen bins, plus a <1- and a >17-Ám bin, are included, although other binning options are available for analysis of coarser-grained sediment. The >17-Ám bin is designated as the "overflow bin" and labeled "9999" (Table T1). Bins are 1 Ám in width, and the number in the "Size" column refers to the lower limit of the range. The Supercount software (version 6.7; Spectrex Corporation, 1998) that accompanies the device also automatically computes the percentages of the total counts, the cross-sectional area, and mass as well as the parts per million in each bin, but these calculations are based on assumptions of concentration, dilution, and particle density as well as shape, which the user must input.
Supercount also calculates the mean grain size and the standard deviation of grain-size distribution. This calculation includes two important assumptions. First, the lower limit of a given bin is taken as the size of all particles in that bin. Using the midpoint of the bin is more representative of the entire bin width than the lower limit (e.g., McBride, 1971). Second, the <1-Ám bin is not considered in the calculations. Since the bins are 1 Ám in width, these approximations may not significantly affect the accuracy of statistics for coarser-grained distributions. Because a large proportion of the particles fall into the <1-Ám bin, eliminating this bin would introduce large errors.
We calculated mean size as
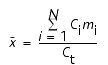
where
We used only the sized grains in calculating CT because the grains in the overflow bin (9999) are undifferentiated by size. These grains may be any size over 17 Ám, which made choosing a midpoint size for this bin impossible. In practice, however, the average counts per cubic centimeter in the overflow bin were <1%, so the associated error is small.
The standard deviation of the grain-size distribution is typically used as a measure of sorting (e.g., Boggs, 1995). We calculated standard deviation,  , by
, by
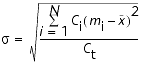 .
.
We used 0.75 Ám as the midpoint of the 0- to 1-Ám bin because of the inability of the laser particle counter to detect particles <0.5 Ám.
We developed a system for running the LPC measurements with fine-grained materials based on repeated testing of standards included with the laser particle counter and natural samples that had been separated by centrifuge. The procedure differs from that recommended by the Spectrex Corporation's instruction manual (Spectrex Corporation, 1998). These choices are summarized in Table T2 and briefly explained below.
The method of agitation is to gently invert the bottle for 30 s at a rate of ~1 cycle every 2 s then allow 15 s of rest prior to scanning in order to eliminate air bubbles. More vigorous agitation introduces excessive air, and less vigorous agitation or a longer rest period allows the larger particles to settle to the bottom prior to scanning. We found this method of agitation preferable to using the magnetic stirrer with which the LPC is equipped. Introducing the stirring magnet into the bottle resulted in a larger number of background counts, especially in the finer size bins. Furthermore, the particles counted are too small to settle to the bottom of the water column during the scan time of 30 s, so the use of the stirring device is unnecessary.
The instrument's threshold controls the smallest particle size to be counted. The wavelength of the light (670.8 nm) limits the smallest resolvable particle to 0.5 Ám, so we placed the threshold at this level (threshold = 7). Lower thresholds result in rapid counting in the absence of any particles because of the effects of light scattering (Spectrex Corporation, 1998). To avoid the effects of light interference at this threshold, it is necessary to shield the exposed upper half of the bottle during scanning. The LPC is equipped with a light shield because ambient light causes interference, but light filtering through the bottle top still causes rapid counting in the <1-Ám bin if a secondary shield is not in place. This problem is eliminated by inverting a cardboard box and placing it over the bottle.
The most troublesome parameter is sediment concentration. When particles interact or drift too close to one another, the LPC measures them as a single large particle. If the concentration is too great, the number of counts in the smaller size bins drops to zero and the resulting grain-size distribution is too coarse. Furthermore, the count rate appears to limit the ability of the instrument to a maximum of ~1000 particles/cm3. Using a restricted range of counts per cubic centimeter is therefore critical. We compared distribution by weight yielded by pipette analysis to counts yielded by LPC scan and found that concentrations near 800 counts/cm3 had the greatest similarity. We also used a centrifuge to make three size splits, <2, 2-4, and >4-8 Ám. Using these fractions of equivalent spherical size, we scanned various concentrations with the LPC and calculated the percentage of counts in the expected ranges. The percentage of particles being counted in the expected range sharply decreased with concentration >750 counts/cm3 for the <2-Ám fraction but sharply increased with concentration >800 counts/cm3 for the 4- to 8-Ám fraction. In order to balance these effects, we chose a concentration of 750-800 counts/cm3 based on similarities between LPC and both pipette and centrifuge results. With concentrations >900 counts/cm3, the percentage of particles <4 Ám in diameter dropped to zero. We interpret this effect to be due to physical interactions between particles. These higher concentrations, though within the range recommended by the manufacturer, can therefore cause the LPC to grossly underrecord the percentage by counts of clay-sized particles.
In order to evaluate the precision of the entire procedure, we randomly selected 24 samples for duplicate runs, wherein the agitation, ultrasonic vibration, dilution, and scanning were repeated. Correlation between repeat runs is 0.84. An F-test reveals that the variances of the two groups of runs are the same, and a Student's t-test demonstrates that the means of the two groups are equal above the 95% probability level (Fig. F5). Twelve runs of the same suspension show that the standard deviation of percentage of counts per cubic centimeter <4 Ám = 1.5% ▒ 2.5%.
In order to standardize the Spectrex laser method to weight percent by settling methods, we correlated the LPC results with the results of pipette analysis. The goal of this analysis is to determine the percent by weight of clay- vs. silt-sized particles in the <63-Ám fraction, with the clay-sized fraction defined as the Stokes' spherical settling equivalent of all particles <4 Ám in diameter.
For constructing the correlation function, the <4-Ám fractions of 20 samples were extracted with the pipette method (e.g., Galehouse, 1971). The same samples were analyzed with the LPC prior to pipetting. Linear regression between the two data sets yields an empirical function for converting the LPC counts to equivalent Stokes' settling diameter (Fig. F5). The correlation coefficient for the two data sets is 0.67, which is significant at the 95% confidence interval. The function is
where
Our comparison shows that the fraction of counts per cubic centimeter by LPC using our method overestimates the weight fraction of clay as compared to spherical settling equivalents.
A second comparison focused on the <2-Ám Stokes' size fraction for the purpose of estimating the absolute abundance of various clays examined by X-ray diffraction analysis. However, regression between the percent of particles <2 Ám by counts and the weight percent of particles <2 Ám by the pipette method was insignificant at the 95% confidence interval (r = 0.44). The lower correlation coefficient is most likely due to the inability of the LPC to resolve particles <0.5 Ám in diameter. Furthermore, very small particles are affected by Brownian movement of molecules in the fluid, so Stokes' Law becomes invalid for particles <0.5 Ám in size (Galehouse, 1971). Particles in the size range below the resolution of the LPC may constitute a significant portion of the sediment; pipette analysis on two randomly selected samples suggests that the <0.5-Ám fraction may be ~20% by weight of the fine fraction and 65% of the <2-Ám fraction for some samples.
Previous studies have demonstrated that when compared to other methods, laser diffraction size analysis is generally accurate, especially when compared to methods based on the measurement of size rather than Stokes' settling. For example, Hall (1988) found no significant differences between results from the Spectrex LPC and the Coulter counter. Similarly, in comparing laser particle counters manufactured by Coulter and Malvern to the Coulter counter TA1, Loizeau et al. (1994) found that results from the laser devices are in good agreement with those of the Coulter counter. However, laser counter results are less similar to settling methods, especially when substantial amounts of clay-sized particles are present. Hall (1988) found that grain-size distribution results by the Spectrex LPC showed a shift toward coarser grains relative to pipette results. Damm (1990) similarly demonstrated a shift of particle size distributions toward coarser grains using the Malvern laser counter relative to results from pipette and Sedigraph techniques, both of which are settling methods.
The agreement between laser particle counter results and those of settling methods decreases when substantial amounts of clay-sized particles are present (Loizeau et al., 1994; Singer, 1988). One reason for differences in the results is a fundamental difference in the dimension measured by laser particle counters and that measured by settling analysis. Whereas the laser particle counter measures the cross-sectional surface of the particles, settling methods measure the weight percent of spherical settling equivalent sizes. Both methods are affected in different ways by particle shape. With a platy particle, the orientation of the particle at the time of measurement affects the LPC results. Nonsphericity as well as particle density also affects settling rates during pipette or similar analyses. Damm (1990) concluded that since platy particles do not conform to ideal spherical settling behavior, the laser particle results are more representative of the true grain-size distribution when platy particles are present.
A second reason for decreased agreement between laser particle sizing and settling velocity methods is the lower limit of size resolution of the laser counter (Loizeau et al., 1994; Singer et al., 1988). The laser device simply does not detect particles below the resolution limit. The pipette technique is also unreliable for measuring the weight percent of particles <0.5 Ám in diameter, but rather than eliminating the particles from analysis as does the laser particle analyzer, the unresolvable fraction is incorporated into the smallest fraction extracted (Galehouse, 1971).
Konert and Vandenberghe (1997) compared the laser particle sizing technique to the pipette technique and showed that the <2-Ám grain size as defined by the pipette method corresponds most closely to the fraction of particles <8 Ám in dimension by counts as defined by the laser sizing technique. Using this larger fraction as the clay fraction would allow comparisons between the two techniques. Their scanning electron microscopy examination of <2-Ám equivalent settling diameter particles revealed that these particles are up to 10 Ám in the long dimension for platy clay mineral grains but with a thickness of <1 Ám. They demonstrated mathematically that grains of these dimensions were the volume equivalent of <2-Ám spheres, and their empirical results are in good agreement with this theory.
Singer et al. (1988) cited physical interactions between clay particles as a reason for underreporting of the abundance of <4-Ám particles by the Malvern laser counter relative to particle-settling techniques. When two particles drift too near one another, the laser particle counter records them as a single large particle, leading to the underreporting of the percentage of counts of finer particles and overreporting of coarser particles. Our technique for fine-grained materials, in contrast to some previous studies, overpredicts the proportion of clay-sized particles relative to pipette analysis. Our strict control on the number of counts per cubic centimeter, in order to avoid physical particle interactions as described previously, is likely the cause of this contrast.
Shipboard data include porosity measurements by the moisture and density techniques (Blum, 1997). Most of the samples for grain-size analysis are within 20 cm of physical property samples. We used the porosity, bulk density, void ratio, and water content of the nearest sample to explore the relation between those properties and grain size.