-
-(dS/dt) = Ae-E
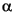/RT [K+]S2,
Smectite is, on average, the most abundant clay-sized mineral at Site 1173 (Table T1; Fig. F2), followed by illite and chlorite (+ kaolinite). Quartz makes up an average of 10 wt% of the <2-µm fraction. Smectite increases downhole from ~20 wt% at the top of the trench-wedge facies to >60 wt% near the top of the lower Shikoku Basin facies (~380 mbsf); from there, smectite gradually decreases to ~35 wt%. The abundance of smectite is erratic in the volcaniclastic facies, ranging from 16 to 82 wt%. The d(060) value ranges from 1.499 to 1.502 Å, demonstrating that the smectite is dioctahedral; it is unknown if the mineral is montmorillonite, beidellite, or a transitional member. As smectite increases in relative abundance, illite declines from ~40 wt% in the trench-wedge facies to ~25 wt% near 380 mbsf in the lower Shikoku Basin facies. Illite then increases to ~35 wt% in two intervals: near 430 mbsf and between 440 and 520 mbsf (Fig. F2). Illite fluctuates erratically in the volaniclastic facies. Chlorite (+ kaolinite) decreases from ~30 wt% at the top of the trench-wedge facies and to ~2 wt% by 380 mbsf. Values increase to ~25 wt% by 400 mbsf and remain fairly consistent to the top of the volcaniclastic facies. Two samples from the lower Shikoku Basin facies show that kaolinite contributes 0% and 12% to the 7-Å peak area (Table T2).
Composite peaks from mixed-layer illite/smectite clays were not detected consistently in samples from above 270 mbsf (Table T1). Starting at 350 mbsf, the percent illite in I/S clays increases from ~15% to 50%, with a maximum of 61%, but there is considerable scatter in the values (Fig. F6). Based on the position of the second-order superstructure, the smectite is disordered. The saddle/peak method does not show any clearly defined changes in I/S with depth (Table T1).
On average, illite and smectite are present in nearly equal amounts at Site 1174 (Table T1; Fig. F3), followed in abundance by chlorite (+ kaolinite). The relative abundance of quartz averages 12 wt%. Smectite abundance increases downhole from ~20 to >55 wt% near 600 mbsf; it then decreases to ~20 wt% by 1100 mbsf. The smectite is dioctahedral, with d(060) values between 1.499 and 1.503 Å. Illite declines from ~35 wt% at the top of the hole to 25 wt% near 650 mbsf. There is a small increase to 35-40 wt% toward the base of the hole. Chlorite (+ kaolinite) decreases from 25 wt% near top of the hole to 10 wt% at ~660 mbsf, then increases below 840 mbsf. The illitic component of I/S mixed-layer clay increases consistently below 590 mbsf, reaching a maximum of 89% (Fig. F6). The gradient in illitization is more pronounced at this site than at Site 1173, but R = 1 ordering does not occur. The saddle/peak method indicates an increase to 45% illite (at 1090 mbsf) (Table T1).
The average relative abundance of smectite at Site 1177 is 51 wt% (Table T1; Fig. F4). Illite averages 27 wt%, chlorite (+ kaolinite) averages 12 wt%, and quartz 11 wt%. The lower Shikoku Basin turbidite facies displays a degree of compositional scatter that is consistent with its lithologic heterogeneity (interbedded turbidites and hemipelagic mudstone). The amount of smectite increases from ~25 wt% at 300 mbsf (upper Shikoku Basin facies) to ~45 wt% at 570 mbsf. Between 570 mbsf and the volcaniclastic-rich facies, smectite varies from 30 to 87 wt%. Smectite content is also erratic in the volcaniclastic-rich facies (27-91 wt%). The smectite is dioctahedral, with d(060) values of 1.499 to 1.503 Å. Illite decreases from ~35 to 20 wt% by 700 mbsf then remains between 15 and 20 wt% to the base of the lower Shikoku Basin turbidites. Chlorite (+ kaolinite) declines from 25 wt% at 300 mbsf to <10 wt% at the base. Based on two samples, kaolinite contributions to the 7-Å peak area are 28% and 60% (Table T2). The I/S mixed-layer clays show no pattern of systematic change with depth (Fig. F6). The percent illite in I/S clays reaches a maximum of 42%, but most values are <25% with random ordering (Table T1).
Placing the clay mineral data in the context of bulk mineralogy is beneficial if the goal is to evaluate whether smectite affects the mechanical and hydrologic properties of the Nankai accretionary prism. To do this, we multiplied the abundance of total clay minerals (using data from the nearest bulk powder sample interval) by the relative weight percent of smectite in the <2-µm clay mineral fraction (where smectite + illite + chlorite = 100%). Although bulk powder XRD methods are imperfect, error analysis shows that the SVD method is accurate to within 5 wt% for standard mineral mixtures (Shipboard Scientific Party, 2001a; Underwood et al., this volume). Nevertheless, our calculated values of mineral abundance in the bulk sediment do not take into account the presence of amorphous solids (e.g., volcanic glass and biogenic silica), and the value calculated for total clay is relative only to quartz, feldspar, and calcite. In addition, clay-fraction data may be affected by mineral partitioning as a function of grain size; this can increase the concentration of smectite in finer size fractions as compared to silt-sized contributions of detrital illite and chlorite (e.g., Mitchell, 1993). Using the <2-µm size fraction probably overestimates the abundance of smectite in bulk mudstone, so the values we report should be considered as maxima for comparative purposes.
Aside from local "spikes" of smectite associated with thin volcanic ash layers, the abundance of smectite in bulk mudstone from Sites 1173 and 1174 is generally <30 wt% (Fig. F7). Depletion of smectite is more extensive in the lower Shikoku Basin deposits at Site 1174. Mudstones from Site 1177, in contrast, contain >30 wt% smectite at virtually all depths in the lower Shikoku Basin facies and volcaniclastic-rich facies; values reach 40-55 wt% near the base of the hole (Fig. F7). The differences in smectite content among coeval deposits at the three sites are probably due to variable amounts of ash-to-smectite and smectite-illite diagenesis.
Many factors influence the smectite-illite reaction, including temperature, potassium concentration in pore water, time, water/rock ratio, fluid and rock composition, the starting composition of the mixed-layer clay, and pressure (Pollastro, 1993, and references therein). The most important of these factors are temperature, heating time, and potassium availability. In one experimentally derived kinetic model, Huang et al. (1993) solved the conversion rate as follows:
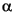/RT [K+]S2,
where,
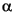= activation energy (28 kcal/mole),
We used this kinetic model to predict the smectite-illite conversion by simulating the evolution of a single packet of smectite as it is buried. Using constraints from shipboard data, calculations were completed at 10-m intervals for Sites 808, 1173, 1174, and 1177.
The assumed starting value for percent illite in I/S was set at 20% illite for each ODP site on the basis of data from shallow burial depths where diagenesis has not yet occurred (Fig. F6). Age-depth relations at each site are sensitive to variations in sedimentation rate and thrusting at the prism toe, so nonuniform burial rates were input into the model. Our choices for age-depth inputs (Table T3) are constrained by paleomagnetic and nannofossil data (Shipboard Scientific Party, 1991, 2001c, 2001d, 2001e; Olafsson, 1993). The potassium concentration for each 10-m interval was taken from the nearest shipboard pore fluid measurement (Shipboard Scientific Party, 1991, 2001c, 2001d, 2001e). Those choices make no allowances for the likelihood of potassium depletion or enrichment through time in response to fluid migration along faults, diffuse flow during consolidation, or in situ mineral reactions. The present-day temperature at each model depth was estimated from shipboard thermal conductivity data and heat flow calculations (Shipboard Scientific Party, 1991, 2001c, 2001d, 2001e; Fisher et al., 1993; Kinoshita and Yamano, 1996). We used a heat flow value of 180 mW/m2 for Sites 1173, 1174, and 808, but a much lower value of 63 mW/m2 was used for Site 1177. We assumed purely vertical conductive and steady-state heat flow, so the modeling ignores the likely effects of thermal decay following the cessation of volcanism along the spreading ridge of Shikoku Basin (Wang et al., 1995).
Figure F6 shows that maximum diagenetic alteration of sediments at Sites 1174 and 808 is less advanced than what model predictions indicate by ~15%-20%. According to one iteration of the kinetic model, illite-smectite diagenesis should reach 94% illite at the base of Hole 1174B, but the maximum illite value measured for the <2-µm size fraction is 84%. At Site 808, illite should reach 98% by the base, but the measured maximum is 78%. This mismatch may be due to rapid tectonic thickening and thrusting near the deformation front, as discussed subsequently. Predictions for Site 1173 are in better general agreement with the observations. The lower temperature gradient at Site 1177 obviously retards the illite-smectite reaction, and modeling predicts no reaction progress (Fig. F6). The calculated geotherm of 53°C/km yields a temperature projection of only 44°C at the base of the hole. The onset of illitization generally occurs between 58° and 92°C (Freed and Peacor, 1989b). Thus, we believe that all of the I/S at Site 1177 is detrital in origin.
