-
k
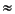 k0[1 – (Pe/P1)m], (5)
k0[1 – (Pe/P1)m], (5)
The grain size distributions are summarized in Figure F3. Grain sizes range from <4 to 50 Ám, and the range of mean sample grain sizes is 3 to 6 Ám. In all of these samples, abundance of grains of a particular size decreases with increasing grain size. The grain size distributions for the four samples from Unit I are very similar. By contrast, the clay from Unit III is dominated by grain sizes <8 Ám. The diatom-bearing radiolarian ooze from Unit II has a grain size distribution intermediate between Unit I and Unit III in that the abundance of very small grains is comparable to that of Unit I, whereas the abundance of larger grains is comparable to Unit III. However, this sample is enriched in 12-Ám grains relative to both the overlying diatom ooze and the underlying clay. Figure F3C shows the grain size distribution relative to the Unit III clay. Here we have assumed that the clay is a background material; then we calculated the fractions of coarser grain sizes that must be added to the clay to obtain the observed grain size distributions of the other five samples. Figure F3C indicates that the biogenic oozes (Units I and II) are enriched in grain sizes between 4 and 24 Ám relative to the underlying pelagic clay.
The permeability data are shown in Figure F4 and are summarized in Table T1.
A first point worthy of note is that our data (Fig. F4) suggest that the permeabilities of these samples vary with effective pressure, as evidenced by the fact that the plots of ln(Pu – Pd) vs. time are not linear; k decreases as the pressure pulse decays. This behavior is a consequence of the fact that permeability depends on the effective cross section or aperture of the channels in the rock, which in turn depend on the effective or applied pressure (e.g., Gangi, 1978). As effective pressure increases, void spaces are compressed and apertures decrease, leading to lower permeabilities. Based on an asperity deformation model, Gangi (1978) has shown that for media containing cracks,
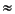 k0[1 – (Pe/P1)m], (5)
k0[1 – (Pe/P1)m], (5)
where k0 is the permeability of the medium at Pe = 0, P1 is a modulus term for the asperities, and m describes the power-law distribution of asperity heights. A fit of this model by Gangi (1978) to experimental data obtained by Nelson (1975), shown in Figure F5, serves to illustrate the effect.
In our experiments, we first apply approximate in situ effective pressure (A in Fig. F5) and then an additional increment of pressure,  P, is added to the upstream reservoir. Thus, at t = 0, the effective pressure at the upstream end of the sample is Pe = Pc – Pp –
P, is added to the upstream reservoir. Thus, at t = 0, the effective pressure at the upstream end of the sample is Pe = Pc – Pp –  P (B in Fig. F5). Hence, the pressure increment has the effect of decreasing the effective pressure and increasing the permeability of the sample by an amount
P (B in Fig. F5). Hence, the pressure increment has the effect of decreasing the effective pressure and increasing the permeability of the sample by an amount  k at the initiation of the test. Subsequently, as the pulse decays, the effective pressure increases, leading to the observed progressive decrease in permeability. Moreover, the highest variation of permeability with effective pressure occurs at low effective pressures. Hence, our samples exhibit this behavior particularly well because the measurements were made at low effective pressures. A complete analysis of this behavior using the transient-pulse method is beyond the scope of this paper. Consequently, our estimates of permeability are based on fits to linear portions of the decay curves shown in Figure F4.
k at the initiation of the test. Subsequently, as the pulse decays, the effective pressure increases, leading to the observed progressive decrease in permeability. Moreover, the highest variation of permeability with effective pressure occurs at low effective pressures. Hence, our samples exhibit this behavior particularly well because the measurements were made at low effective pressures. A complete analysis of this behavior using the transient-pulse method is beyond the scope of this paper. Consequently, our estimates of permeability are based on fits to linear portions of the decay curves shown in Figure F4.
Estimated permeabilities of the diatom oozes from Unit I range from 534 to 1604 Ád, whereas the permeability of the radiolarian ooze from Unit II is slightly lower (289 Ád) and the permeability of the Unit III pelagic clay is two orders of magnitude lower (~1.9 Ád) (see Table T1).
Figure F6 is a plot of log(k) vs. porosity for our samples. Also shown are the data for diatomaceous sediments from the Weddell Sea (Bryant and Rack, 1990). Although there is a clear correlation between log(k) and  (R = 0.99), the relationship is not necessarily linear because the data from Units I and II lie in a cluster. The data for samples from Units I and II alone lie on a similar trend, but the correlation is lower (R = 0.87) and significant at the 0.06 level but not at the 0.05 level.
(R = 0.99), the relationship is not necessarily linear because the data from Units I and II lie in a cluster. The data for samples from Units I and II alone lie on a similar trend, but the correlation is lower (R = 0.87) and significant at the 0.06 level but not at the 0.05 level.
While the effect is difficult to quantify from the available data, there is also an apparent relationship between permeability and grain size among our samples. Figure F3C suggests that the sample with the highest proportion of coarser grain sizes (from Core 191-1179C-10H) also has the highest permeability, followed in order by the samples from Cores 15H, 19H, 4H, 21H (Unit II), and 24H (Unit III). Although they lie on a similar trend, our samples have appreciably lower permeabilities than the samples from the Weddell Sea, relative to their porosities. The reason for this difference is probably related to the diatom contents of the sediments. The sediments from Unit I at Site 1179 contain 40%–60% diatoms, whereas all of the samples from the Weddell Sea with porosities >75% contain more than 80% diatoms (Bryant and Rack, 1990).