- cm
= the vertical compressibility,
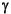 = the loading efficiency,
= the loading efficiency,
 z
= the axial load, and
z
= the axial load, and
- D = the hydraulic diffusivity.
These data were analyzed to determine estimates of hydraulic conductivity and specific storage using two different methods, the square root of time method and a variable-thickness deformable-element finite difference routine. Estimates of hydraulic conductivity and specific storage were found by fitting curves produced by these models to the data. Figure F4 shows data from one of the runs on Sample 195-1200E-5H-3, 51-61 cm, and curve fits of the two methods of analysis, square root of time (Fig. F4A) and finite difference (Fig. F4B). The square root of time method is quickly and easily applied but involves more assumptions, whereas the finite difference method, although more cumbersome, removes some assumptions.
To analyze the data using the square root of time method, we use the relationship for displacement in a semi-infinite length cylinder as a function of time (Terzaghi, 1943; Taylor, 1948; Wang, 2000), as follows:
where,
We can determine the lumped product of constants on the right hand side of Equation 3 by calculating the slope of the displacement vs. the square root of time, as follows:
Only the early time
portion of the plot, from 0 to 2500 s, is used to determine the slope (Fig. F4).
The rest of the data points from 3000 to 9000 s are neglected. At early times,
the pore pressure decrease has not yet diffused to the end of the sample (see
Fig. F2) and so
the approximation of a semi-infinite cylinder is still valid. To determine the
hydraulic diffusivity (D) from the lumped product in Equation 3, we
need to determine the other unknown factors of the lumped product, cm
and ![]() .
.
The vertical compressibility is defined by the following equation:
Because all the components
of Equation 4 (axial displacement [![]() w],
axial stress [
w],
axial stress [![]() z],
and sample length [w0]) were measured, it is possible to
calculate the vertical compressibility. Also, the conditions of no radial strain
(err = 0) and no change in pore pressure (
z],
and sample length [w0]) were measured, it is possible to
calculate the vertical compressibility. Also, the conditions of no radial strain
(err = 0) and no change in pore pressure (![]() Ppore
= 0) were valid because the stiff cylinder wall prevented radial strain and the
pore pressure throughout the entire length of the sample returns to atmospheric
pressure at very long times. However, the assumption of infinitesimal strain is
not well met in these measurements. The estimated strain for the sample whose
data are shown in Figure F4
is ~20%, a typical value for these tests.
Ppore
= 0) were valid because the stiff cylinder wall prevented radial strain and the
pore pressure throughout the entire length of the sample returns to atmospheric
pressure at very long times. However, the assumption of infinitesimal strain is
not well met in these measurements. The estimated strain for the sample whose
data are shown in Figure F4
is ~20%, a typical value for these tests.
The loading efficiency is defined as the following:
where Ppore
= the pore fluid pressure. The assumption of incompressible grains and pore
fluid lead to a value for ![]() of 1 (Wang, 2000). Given that cm and
of 1 (Wang, 2000). Given that cm and ![]() have been determined, the hydraulic diffusivity (D) can be calculated
using Equation 3.
have been determined, the hydraulic diffusivity (D) can be calculated
using Equation 3.
Assuming the grains and pore fluid are incompressible, the specific storage (Ss) can be calculated by the following equation:
Ss = cm xwhere,
Finally, we can determine the hydraulic conductivity (K) from the hydraulic diffusivity and specific storage using Equation 7:
K = D x Ss. (7)This method suffers from having to make the assumption of a semi-infinite cylinder and then making the decision of how much of the data to include when calculating the slope to estimate the lumped product of constants in Equation 3. In Figure F4, we chose to include only those data recorded from 0 to 2500 s, but that decision was subjective. The second method of data analysis, finite difference, does not assume a semi-infinite cylinder, nor does it assume that the strains are infinitesimal. The sample deforms in response to the amount of fluid that has been discharged.
The finite difference
method removes the need for assuming a semi-infinite cylinder and incorporates
the shortening of the sample (finite strains) as pore fluid drains from the
sample bottom. Like the square root of time method, it assumes that the grains
and pore fluid are incompressible so that ![]() = 1 and Equation 6 is valid. Inputs for this routine are initial guesses for the
hydraulic conductivity and the specific storage and measured values for the
final sample length, the applied axial load, and the area of the cylinder. Using
Equations 4, 5, and 6 and the specific storage estimate supplied by the user,
the initial length of the sample is calculated. It is this calculation that will
ultimately constrain the value of the specific storage. Using this initial
length, the sample is divided into 25 elements by the finite difference routine.
Initial head values are input by setting the head at the sample bottom equal to
zero and by setting the heads throughout the rest of the model equal to values
calculated using Equation 5 and the applied axial load, as follows:
= 1 and Equation 6 is valid. Inputs for this routine are initial guesses for the
hydraulic conductivity and the specific storage and measured values for the
final sample length, the applied axial load, and the area of the cylinder. Using
Equations 4, 5, and 6 and the specific storage estimate supplied by the user,
the initial length of the sample is calculated. It is this calculation that will
ultimately constrain the value of the specific storage. Using this initial
length, the sample is divided into 25 elements by the finite difference routine.
Initial head values are input by setting the head at the sample bottom equal to
zero and by setting the heads throughout the rest of the model equal to values
calculated using Equation 5 and the applied axial load, as follows:
To calculate the heads at subsequent time steps, the explicit finite difference approximation was used, although the Crank-Nicolson approximation (Wang and Anderson, 1982) might also have been employed. Following each time step, the length of each element was recalculated using the following definition of storativity (specific storage multiplied by element length) and the assumptions of incompressible grains and pore fluid:
where,
These new model lengths were then used in the next time step to calculate the heads at the next time step.
The outflow at the sample bottom (Qn) was also calculated at each time step (n) using the following equation:
Qn = -area x K(where ![]() h1
and
h1
and ![]() x1
are the head and element thickness, respectively, of the bottom element. The
heads at the nodes and the outflow at the sample bottom for each time step were
recorded as the model stepped through time. When the model reached the end time,
set to be after the last recorded data point for the sample, the model results
for the outflow and data of outflow were plotted on the same graph and compared.
The initial guesses of the hydraulic conductivity and specific storage were then
varied to improve the fit and the model was rerun until a satisfactory fit
between the model and the recorded data was found. A formal inversion could be
implemented to better fit the data and give sensitivities of the hydraulic
conductivity and specific storage to the data.
x1
are the head and element thickness, respectively, of the bottom element. The
heads at the nodes and the outflow at the sample bottom for each time step were
recorded as the model stepped through time. When the model reached the end time,
set to be after the last recorded data point for the sample, the model results
for the outflow and data of outflow were plotted on the same graph and compared.
The initial guesses of the hydraulic conductivity and specific storage were then
varied to improve the fit and the model was rerun until a satisfactory fit
between the model and the recorded data was found. A formal inversion could be
implemented to better fit the data and give sensitivities of the hydraulic
conductivity and specific storage to the data.
A check was performed to
ascertain that the cumulative discharge (![]() NQn),
determined by summing the discharges calculated in Equation 10, was still equal
to displacement, calculated by summing the length of all the elements at time
step n, multiplied by the area. The two results agreed to better than
0.1% difference.
NQn),
determined by summing the discharges calculated in Equation 10, was still equal
to displacement, calculated by summing the length of all the elements at time
step n, multiplied by the area. The two results agreed to better than
0.1% difference.