- P (
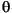 ,
, )
d
)
d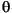 d
d = (
= (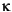 /4
/4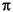 sinh
sinh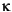 )
exp (
)
exp (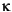 · cos
· cos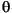 )(sin
)(sin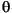 )
d
)
d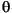 d
d ,
,
Paleomagnetic and rock magnetic investigations during Leg 197 were focused on obtaining inclination data that could be used to derive preliminary estimates of (1) the time intervals recorded by the basaltic sequences drilled, (2) the paleolatitude of the Emperor Seamounts (Detroit, Nintoku, and Koko Seamounts), and (3) the relative contributions of induced and remanent magnetizations in the basement rocks. This was accomplished by the routine measurement of natural remanent magnetization (NRM), detailed alternating-field (AF) demagnetizations and subsequent remanence measurements, and measurements of magnetic susceptibility. These measurements were mainly conducted on discrete samples taken from the working core halves.
Detailed stepwise AF demagnetizations were performed to isolate characteristic remanent magnetization (ChRM) components and to quantify magnetic overprints. Characteristic directions were fit using principal component analysis (Kirschvink, 1980). ChRM inclinations from the samples of each igneous flow unit were averaged following the method of McFadden and Reid (1982). A potential problem in obtaining paleolatitude data from any basalt drill hole is the uncertain timescale between eruptions. If most flows reflect rapid eruptions, one could easily obtain a biased paleolatitude estimate by giving equal weight to each flow unit. To address this concern, the inclination-only averages derived from each flow unit were checked for serial correlation using geological constraints provided by visual core descriptions, thin section analyses, and geochemical analyses (see "Physical Volcanology and Igneous Petrology").
Independent paleomagnetic inclination groups determined from these analyses were used to estimate the angular dispersion recorded by the data (Tarduno and Sager, 1995; Tarduno and Cottrell, 1997). This was done by transforming the directional angular dispersion, estimated from the inclination groups, into geomagnetic pole space (Cox, 1970). These estimates of angular dispersion were compared to global data syntheses (McFadden et al., 1991) to determine whether a given basement section sampled sufficient time (over several thousand years) to average geomagnetic secular variation. Inclination units were further averaged to calculate mean paleolatitudes and 95% confidence intervals.
In addition to the measurements of discrete basalt samples discussed above, select sediment cores were analyzed. These investigations included pass-through measurements of NRM of both archive-half cores and discrete samples from the working-half cores. Select AF demagnetizations were also performed. The measurement technique applied to the sediment cores varied as a function of core recovery and disturbance.
The remanence of archive-half sections and oriented discrete samples from the working-half sections was primarily measured using a pass-through 2-G Enterprises DC-superconducting quantum interference device (SQUID) rock magnetometer (model 760R). The magnetometer is equipped with an in-line AF demagnetizer (2-G model 2G600), where samples can be demagnetized to peak fields of 80 mT. Both the magnetometer and AF demagnetizer are interfaced with a PC-compatible computer and are controlled by the 2-G Long Core software (Core Logic). Some discrete samples were also measured using a Molspin Minispin spinner magnetometer. A model D-2000 DTech Inc. AF demagnetizer was used for stepwise demagnetization of the discrete samples measured with the Molspin magnetometer. The DTech AF demagnetizer is capable of peak fields up to 200 mT.
Low-field magnetic susceptibility was measured for select sediment whole-core sections using a Bartington Instruments model MS2 susceptibility meter attached to the MST (see "Physical Properties"). The susceptibility sensor for whole-core measurements (MS2C) has an 88-mm coil diameter, and the core passes through the sensor. Magnetic susceptibilities for discrete samples were measured using either a Geofyzika Brno Kappabridge KLY-2 magnetic susceptibility meter or a Bartington Instruments model MS2 susceptibility meter. Select samples were chosen for measurement of anisotropy of magnetic susceptibility with the KLY-2.
Test samples with known magnetic directions and intensities from the University of Rochester were used to test the calibration of the 2-G SQUID and Molspin Minispin magnetometers. Calibration samples were available on board for the Molspin magnetometer, the Bartington susceptibility meter, and the Kappabridge magnetic susceptibility meter. Samples that were measured with the 2-G SQUID magnetometer were also measured with the Molspin magnetometer to check for consistency between the two instruments. The base level of the 2-G SQUID magnetometer is measured to be on the order of 0.0001 A/m.
The shipboard 2-G SQUID magnetometer is currently configured to measure up to seven discrete samples (each sample was separated from its nearest neighbor by 20 cm) on a 150-cm-long sample tray. However, the magnetometer averages over a 20-cm region. Thus, strongly magnetized samples (such as basalt) can influence adjacent samples measured on the 2-G SQUID if they are not separated by a sufficient space. To test this effect, background measurements were made on the sample pass-through track and compared against empty sample spaces 10, 20, 30, and 40 cm away from a strongly magnetized test sample. We found that a 40-cm space between discrete samples on the pass-through sample tray was required to avoid spurious signals introduced by adjacent samples. This spacing allowed four samples to be measured at a time. Strongly magnetized samples may also influence the SQUID electronics, causing flux jumps that bias data recording. To avoid flux jumps resulting from samples with very strong magnetizations (>15 A/m intensity), the velocity of the track as it passes through the sensor coils was reduced from 25 to 5 cm/s.
Standard samples of known magnetization from the University of Rochester were used to calibrate the Molspin Minispin magnetometer. Short spins (corresponding to 24 revolutions, for which the output signal is integrated) in four positions were used to obtain one magnetization measurement using the Molspin magnetometer. After calibration, the values of magnetization intensity, declination, and inclination for the standards and several test samples were in good agreement (within 5%) with the values obtained using the 2-G SQUID magnetometer. The background level for the Molspin magnetometer was found to be ~0.001 A/m.
Both the Bartington susceptibility meter and the KLY-2 Kappabridge susceptibility meter were used for low-field susceptibility measurements, whereas only the Kappabridge was used for anisotropy of magnetic susceptibility measurements. The KLY-2 Kappabridge was calibrated using a standard sample of known susceptibility. To check the accuracy of the Bartington susceptibility meter, we measured susceptibilities of a few samples using the Kappabridge and compared them to the values given by the Bartington susceptibility meter. We found that the Bartington susceptibility meter gives susceptibility values in fairly good agreement (within 5%-10%) with the values measured using the Kappabridge.
The standard ODP core orientation convention (Shipboard Scientific Party, 1991, fig. 8; Shipboard Scientific Party, 1997a, fig. 8) was applied for paleomagnetic work during Leg 197 (Fig. F21). This convention is as follows: the z-axis of the sample is downhole parallel to the z-axis of the drill core. The split face of the drill core represents the y-z plane. The x-axis is then the line perpendicular to the split face (y-z plane) and is directed into the working half of the core. The x-axis is used as the reference for the relative definition of the remanence vector. Discrete samples were taken from sediment and basalt rocks by drilling cylindrical minicores (10 cm3) with a water-cooled drill bit attached to a standard drill press. Minicores were oriented with an arrow on the split face (y-z plane) pointing in the uphole direction (-z).
Discrete samples were demagnetized using alternating fields ranging from 0 to 80 mT at 5-mT steps for the first 50 mT and then at 10-mT steps for the remaining treatments to isolate stable remanence components in the samples for Sites 1203 and 1204. For Sites 1205 and 1206, samples were demagnetized at 5-mT steps for the first 70 mT and then at 10-mT steps for remaining treatments. The stability of remanence was determined using orthogonal vector plots (Zijderveld, 1967) and equal-area projections, and ChRM directions were obtained using principal component analysis (Kirschvink, 1980). Four to six discrete minicore samples were drilled from each basalt cooling unit to evaluate intraflow directional stability.
ChRM inclinations for each basalt unit were averaged using the method of McFadden and Reid (1982). This approach utilizes a maximum likelihood estimate to limit bias in inclination averages. The general solution for the maximum likelihood estimate is dependent on the assumption that the inclinations examined are drawn from a Fisher distribution (Fisher, 1953) defined by:
where,
ChRM inclination values from each independent inclination group were averaged (McFadden and Reid, 1982) to obtain an overall site inclination. The best estimate of the dispersion parameter (k) was used to estimate directional angular dispersion (s) as follows (Butler, 1992):
Estimates of directional angular dispersion were further transformed into estimates of pole dispersion (S) using the numerical values of Cox (1970). Values of S allowed us to compare our data with global paleomagnetic data sets derived from lavas to assess the averaging of secular variation in the recovered basalt sequences. We note, however, that we have made no attempt to adjust S for inclination dispersion within each basalt flow in our preliminary analysis. We utilized the reference curves of McFadden et al. (1991), which describe virtual geomagnetic pole scatter in terms of primary (Sp) and secondary (Ss) geodynamo families:
The 43- to 81-Ma time
interval was of interest for the drill sites analyzed. For the 45- to 80-Ma
interval, Ss = 9.7° ± 1.5° and Sp/![]() = 0.34 ± 0.03, where
= 0.34 ± 0.03, where ![]() is the paleolatitude. For the 80- to 110-Ma interval, Ss =
6.5° (+2.9°/-4.2°) and Sp/
is the paleolatitude. For the 80- to 110-Ma interval, Ss =
6.5° (+2.9°/-4.2°) and Sp/![]() = 0.33 ± 0.05 (Fig. F22).
Paleolatitudes for each site were calculated from the geocentric dipole
relationship:
= 0.33 ± 0.05 (Fig. F22).
Paleolatitudes for each site were calculated from the geocentric dipole
relationship:
where I is the average of the inclination groups.
Bulk magnetic susceptibility data and NRM intensities were used to calculate the ratio of remanent to induced magnetization, or Koenigsberger ratio (Q):
where,
The calculated Koenigsberger ratios provide important input into the interpretation of magnetic logging of the basalt sections (see "Downhole Measurements").
Rock magnetic properties, through the use of Lowrie-Fuller tests (Lowrie and Fuller, 1971) and coercivity of remanence, were also measured to assess magnetic domain state and magnetic hardness. The Lowrie-Fuller test can be used as a rapid determination of domain state in igneous rocks. It is based on the observation that multidomain grains require a larger destructive field to demagnetize a thermoremanent magnetization (TRM) acquired in a strong field. A laboratory-induced saturation remanent magnetization (SIRM) acquired in a 0.8-T field using an IM-10 impulse magnetizer represents the strong-field TRM. The demagnetization of the SIRM is compared with the demagnetization of a weak-field TRM, here represented by an anhysteretic remanent magnetization produced by demagnetizing the sample in a 140-mT alternating field in the presence of a 30-mT direct-current (DC) field. AF demagnetizations were done with the D-2000 AF demagnetizer, and all remanences were measured with the shipboard Molspin Minispin magnetometer.
Isothermal remanent magnetization (IRM) acquisition and backfield IRM acquisition were measured to derive coercivity of remanence, an estimate of magnetic hardness. Stepwise IRMs were imparted in the +x direction (sample coordinates) using an IM-10 impulse magnetizer until the saturation remanence (Mrs) was reached. Then the samples were DC demagnetized by giving them a stepwise IRM in the -x direction. The remanence decreases to zero at the coercivity of remanence (Hcr) and culminates in -Mrs, the negative saturation remanence.
In addition to the paleomagnetic and rock magnetic study of basalt, volcaniclastic, and sedimentary minicores, magnetozones were defined on the rotary-cored consolidated sediment units. Polarities of core samples were determined on the basis of consistent ChRM directions obtained from a >10-cm-long portion of core, either using archive halves or discrete samples. The magnetic polarity stratigraphy was then interpreted using constraints from the biostratigraphic data (see "Biostratigraphy"). The numerical ages of Cande and Kent (1995) were adopted (Table T9; Fig. F23).