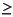0.03 wt% C.
Calcium carbonate and organic carbon were determined by coulometry at Boise State University (BSU; Idaho, USA) using a UIC, Inc. model CM-5012 CO2 coulometer attached to our modified version of a CM-5120 combustion furnace. See Olivarez Lyle and Lyle (this volume) for special notes regarding the Corg analysis. Approximately 30–70 mg of dried, homogenized sediment sample was combusted in an ultra-high-purity oxygen (>99.994% O2) atmosphere at 1000°C. The reported CaCO3 data were calculated as the difference between two independent analyses of carbon from each sampled interval. First we measured the total carbon concentration of an untreated sediment sample, followed by a second analysis of a sample aliquot after pretreatment with 10% hydrochloric acid solution to dissolve solid CaCO3. Inorganic carbon was calculated as the difference between the total carbon and the Corg fractions. The amount of CaCO3 (in weight percent) is the product of inorganic carbon (in weight percent) and 8.33.
An additional set of samples was run for CaCO3 at Stockholm University (Sweden) using a UIC coulometer with an acidification module. A subset of the Stockholm samples was also run at both laboratories, and results of the interlaboratory comparison showed no systematic differences between the two laboratories. The Stockholm samples (marked J. Backman) are interleaved with the BSU analyses in Tables T1 and T2.
Corg was measured at BSU after the sample was pretreated with acid to remove carbonates. Approximately 70 mg of dried sample was placed inside a fused quartz combustion boat and then wetted with water and 10 drops of 10% HCl. The slurry was stirred and heated at ~110°C until sufficient solution evaporated to accommodate a second treatment with the acid. After ~1 hr, samples were oven-dried and allowed to cool before analysis with the coulometer.
Accuracy was estimated by including two independent standards in each sample run, and precision was estimated by repeating the analyses of a subset of the unknown samples. As standards, we used a reagent-grade calcium carbonate or reagent-grade sucrose and an in-house standard, Midway, a marine sediment from the northeast Pacific Ocean. Precision of the unknowns was estimated by repeating the analysis of every fourth sample in the sample run. The average difference between the repeated samples is <0.01 wt% carbon. In general, samples were reanalyzed if the difference between the repeated analyses was 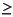0.03 wt% C.
Biogenic silica was measured by spectrophotometry after samples were digested in a 2-M KOH solution. The method is summarized below and discussed in great detail in Olivarez Lyle and Lyle (2002), a laboratory study designed to address the long-standing problem of measuring dissolution-resistant radiolarians in Eocene and Miocene marine sediments. There are two parts to the analytical problem: first, the widely used Mortlock and Froelich (1989) method, which employs a 2-M sodium carbonate bath, is ineffective at dissolving the Eocene radiolarians, as was shown for Leg 199 site survey sediments. Second, the pervasive assumption that clays are dissolved during the alkaline bath and therefore contribute significant amounts of dissolved silica to the result leads to an overestimation of the opal content of sediments. Olivarez Lyle and Lyle (2002) show that the harsher KOH treatment can successfully dissolve the biogenic silica component without compromising the analysis via clay dissolution.
Approximately 20–50 mg of dried sample was pretreated with hydrogen peroxide and hydrochloric acid to remove organic matter and carbonates. After this pretreatment, samples were rinsed, decanted, and oven-dried. Then, 20.0 mL of a 2-M KOH solution was added to samples in centrifuge tubes, including blanks, which were then capped, sonified, and weighed. Samples were placed in a covered shaking water bath and digested at 85°C. The samples in tubes then were centrifuged and allowed to cool for ~1 hr before analysis. Dissolved silica was measured by the heteropoly blue method using a Hach DR/4000 spectrophotometer following sample dilution with deionized, distilled water, following a standard procedure for low-range silica (Hach Method 8186).
Two standards were used for the opal analysis: a reagent grade dissolved silica standard (Hach 1106-49) and either the 1218C composite standard or the 1219A composite standard, both in-house sediment standards from Leg 199. These sediment standards were made by combining subsamples of equal mass from every sample we analyzed from each site. Therefore, the composite sediment standard should reflect all site-hole variation in biogenic silica and matrix materials. Summary statistics for the composite sediment standards are as follows: 1218C composite standard average = 32.2 ± 2.0 wt% SiO2 (n = 87) and 1219A composite standard average = 56.3 ± 1.7 wt% SiO2 (n = 52). In certain cases, a diatom ooze sediment standard was used from ODP Leg 178 Site 1098 (average = 31.2 ± 1.4 wt% SiO2; n = 14) because an existing database using our laboratory method had been established (Olivarez Lyle and Lyle, 2002). Generally, every sample was analyzed twice and every fourth unknown sample was replicated in the same run (as samples in separate tubes). Samples were reanalyzed in a later run if the difference between the repeated analyses exceeded ±8 wt% SiO2. Note that reported biogenic silica data have not been corrected for structural water content, which can be as high as 15 wt% in radiolarians.
We analyzed 109 samples from Site 1219 for bulk carbonate oxygen isotopes at Stockholm University. The samples were first run for CaCO3, and samples that contained >10 wt% CaCO3 were sent for analysis. The samples were dried and powdered, and then a 100- to 150-g sample was placed in a Kiel carbonate preparation device and analyzed on a Finnegan MAT mass spectrometer. Analytical precision is better than 0.1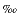
.
To account for differences in the mass of material preserved per unit time and the differential compaction of downcore intervals, we converted all linear sedimentation rate data to mass accumulation rates (MARs) for all intervals. MAR is defined as the product of the linear sedimentation rate (LSR; length/time) and the dry bulk density (DBD; mass/volume) and has units of [mass/(unit area x unit time)]. DBD is related to wet bulk density (WBD) by the following equation:
H2O),
where P is pore fraction and H2O is the water density.
Because the multisensor track (MST) measures wet bulk density at the centimeter scale, there are ~2 orders of magnitude more data for WBD than DBD. We took advantage of the added resolution of the WBD data by estimating DBD from WBD. The shipboard moisture and density measurements of these parameters were used to define linear regression equations which relate DBD as a function of WBD. Subsequently, the appropriate equation, based on a relatively low resolution of samples, was applied to the shipboard gamma ray attenuation (GRA) wet bulk density measurements, spaced every 2 cm for our samples, to generate a high-resolution DBD data set. We used the stacked WBD data assembled by H. Pälike (unpubl. data) as the basis for the DBD data set.
For each site, correlation coefficients were very high (r = 0.997) for the low-resolution linear regression generated when all of the data were utilized (i.e., all lithologic units) (Olivarez Lyle and Lyle this volume). However, better correlations, along with different regression equations, were obtained when the regressions were generated based on major lithologic units identified for each drill site. Ultimately, we decided to use the regression equations based on lithology to predict the DBD value (and resulting MAR) rather than using a single equation for each site. This decision is justified by the magnitude of the differences in the predicted DBD values that resulted from the lithology-based equations. The difference was particularly important for the Eocene radiolarian ooze and clay section. DBD calculated using the regression based upon lithology was significantly closer to the measured DBD and systematically 7% higher than DBD calculated by the site average regression.
