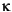) but by mobility (m), which is the ratio of permeability to fluid viscosity (µ) (Qobi et al., 2001; Brie et al., 2000). In general, µ is known and more or less constant within one borehole so that m can be taken as a proxy for .
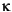In this section we describe basic features of acoustic wave propagation in boreholes and introduce characteristics of the Stoneley wave. The standard data processing to derive wave velocity as well as our additional processing to yield energy content is explained.
In a borehole, an acoustic source pulse disintegrates into a number of discrete mode peaks with successively increasing frequencies (Paillet and Cheng, 1991) and generates complicated interference patterns. Classical theory predicts a full wave train consisting of a head P-wave, a head S-wave, guided waves including a number of normal modes, and a Stoneley wave (Chen, 1982). Their features are summarized in Table T1; a detailed description of the great number of complex wave types generated in boreholes can be found in Paillet and Cheng (1991, 1986) and Paillet and White (1982).
We focus on the Stoneley wave, which is the fundamental mode of guided waves (Winkler et al., 1989; Paillet and Cheng, 1991). Its wave motion is an expanding/contracting borehole motion (Qobi et al., 2001), illustrated in Figure F3. The radial component of the Stoneley wave forces fluid into fractures, which results in a loss of energy (i.e., decrease of amplitude), and this effect is responsible for the sensitivity of Stoneley waves to permeability.
Stoneley waves are not directly affected by permeability (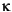) but by mobility (m), which is the ratio of permeability to fluid viscosity (µ) (Qobi et al., 2001; Brie et al., 2000). In general, µ is known and more or less constant within one borehole so that m can be taken as a proxy for .
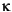Permeability can influence Stoneley wave propagation in three ways. Stoneley waves can be partly reflected at sharp impedance contrasts (Gelinsky et al., 1998; Brie et al., 2000) such as fractures, lithology, or borehole diameter changes. Moreover, as formation permeability increases, Stoneley wave velocity decreases (Winkler et al., 1989), thereby inducing dispersion. The third effect is the attenuation of Stoneley waves, which we investigate in this paper.
Attenuation occurs when fluid is pressed into the permeable formation and energy is lost in the relative motion between viscous pore fluid and the elastic solid matrix (Norris, 1989). Attenuation therefore correlates with permeability, but unfortunately, lithologic boundaries or variable borehole geometry also attenuate Stoneley waves (Paillet and White, 1982). Consideration of other logging and core measurements is necessary to distinguish between the possible causes of the observed attenuation. Modeling the geometric effect is essential for a quantitative meaningful interpretation but is of minor importance if only qualitative changes of downhole permeability are derived.
The DSI tool is a full waveform acoustic logging tool that delivers measurements of sonic wave propagation in a wide variety of formations (Shipboard Scientific Party, 2003c). This tool, illustrated in Figure F4, consists of a linear array of eight receiver stations spaced 15.24 cm (6 in) apart and two different transmitters (Lamont-Doherty Earth Observatory–Borehole Research Group Wireline Logging Services Guide [LDEO-BRG, 2000]). The monopole transmitter with an omnidirectional source characteristic generates a high-frequency pulse (~14 kHz, called P&S mode) for P and S head waves and a low-frequency pulse (~1 kHz, called Stoneley mode) for Stoneley wave excitation. The two dipole transmitters that create nonaxisymmetric signals drive a low-frequency pulse (~2 kHz) for flexural wave excitation, which is normally used to estimate shear wave velocity in highly unconsolidated formations. Each receiver station contains two hydrophone pairs oriented perpendicular to each other and parallel to the upper and lower dipole transmitter.
In the acquisition cartridge, the waveforms undergo automatic gain control and are digitized (12-bit dynamic range). A 40-µs sampling interval is used for the low-frequency Stoneley and all dipole modes and 10 µs for the higher frequency P&S mode. Each record consists of 512 samples, resulting in a record length of ~20 ms for Stoneley waves and ~5 ms for P- and S-waves.
Standard processing of acoustic records comprises a waveform correlation of the digital signals to find coherent arrivals across the receiver array. Waveform correlation consists of an analysis of semblance, which is a measure of correlation between waveforms that takes into account both signal shape and amplitude and which is used to find coherent arrivals of a wave traveling in a medium (i.e., Taner and Koehler, 1969; Kimball and Marzetta, 1984). It is a function of arrival time at near-receiver and acoustic wave velocity and ranges between 0 for noncorrelated signals and 1 for perfectly correlated waveforms. Standard processing calculates semblance for all sensible combinations of arrival time and wave velocity and identifies local maxima of semblance in the following picking and labeling process. The corresponding velocity and energy are stored, and the procedure is repeated for each source shot to create velocity and energy depth profiles.
The routine processing of DSI data onboard the JOIDES Resolution is performed by the engineer on a Schlumberger MAXIS system, and final processing is done on GeoFrame at LDEO (Shipboard Scientific Party, 2003c). This processing comprises a waveform correlation (slowness time coherence [STC]) providing the acoustic wave velocities (VP , VS, and VStonely) that are then available in the database. However, the energy content of the identified waves was not available for the Leg 205 data.
Because our research focused on the analysis of Stoneley wave attenuation, we subjected the Stoneley waveform data to semblance analysis to yield energy estimates. We used the algorithm reported in Kimball and Marzetta (1984) and implemented it in Matlab, extended by the capability to store arrival time and to calculate the energy contained in the detected arrival. Again following Kimball and Marzetta (1984), we considered as an energy estimate the power in the trace stacked with the identified wave velocity. Tests on synthetic data overlain with random noise have proven that the algorithm identifies arrivals with the accuracy in the range of the algorithm's velocity resolution.
