METHODS
One-dimensional incremental load consolidation tests provide key parameters for reconstructing the stress history of clayey marine sediments (Terzaghi, 1943). Testing is performed by incrementally loading a sample to levels that exceed the expected in situ effective stress ( ´) and allowing the pore pressure to dissipate as the sediment settles. The change in sample height under each new load is used to calculate the volumetric strain or void ratio (e) at the end of each step and defines the sediment's compressibility. Because soils are not perfectly elastic, the deformation behavior they exhibit depends on the stress history of the sample. This allows four critical parameters to be derived from a consolidation test:
´) and allowing the pore pressure to dissipate as the sediment settles. The change in sample height under each new load is used to calculate the volumetric strain or void ratio (e) at the end of each step and defines the sediment's compressibility. Because soils are not perfectly elastic, the deformation behavior they exhibit depends on the stress history of the sample. This allows four critical parameters to be derived from a consolidation test:
- The compression index (Cc), which defines the sediment compressibility as the slope of the e-log(
 ´) curve during loading;
´) curve during loading;
- The recompression index (Cr), which is the slope of the e-log(
 ) curve during unloading;
) curve during unloading;
- The preconsolidation pressure (Pc´), interpreted as the maximum past effective stress that the sediment has experienced and calculated using the curve fitting method of Casagrande (1936); and
- The void ratio of the sediment upon deposition (eo) (Fig. F4) (Moran et al., 1995; MacKillop et al., 1995).
In addition to these four parameters, the time deformation behavior of the sediments can be used to determine the relationship between permeability and void ratio for the sediment.
Whole-round samples, taken shipboard from visually undisturbed sections of core, were sealed with wax, immersed in seawater, and kept refrigerated at 4°C after being shipped to the Marine Geomechanics Laboratory (University of Rhode Island). Prior to testing, the samples were removed from the sealed core liner and trimmed to a standard height of 2 cm and a diameter of 4.97 cm. Once trimmed, the wet mass of the sample was recorded before the sample was transferred into the consolidation cell that is immersed in de-aired, ultraviolet-treated seawater taken from Narragansett Bay, Rhode Island. The cell is constructed of stainless steel and allows sediment deformation to occur only vertically. The sample is set within the cell and placed between two porous stones. Saturated filter papers are used to separate the sample from the porous stones and prevent fine-grained sediment particles from blocking the drainage paths through the stones. After the cell is assembled, it is transferred to the consolidometer, where testing begins. General sample preparation and testing procedures followed the guidelines set out by the American Standards and Testing Materials (ASTM) standard D2435-04 (ASTM International, 2007). One-dimensional incremental load consolidation tests were conducted using one of two instruments: (1) an ELE International lever arm consolidometer or (2) a fully automated Loadtrack consolidation frame and data acquisition software system manufactured by Geocomp. Using the selected sample diameter, both systems were capable of applying loads of as much as 10 MPa.
The Geocomp assembly continuously monitors and records variations in both the applied load and sediment height. Prior to the start of each test, the loading sequence is entered into the software, with both a maximum and minimum time specified for the duration of each step. For this testing program, the Geocomp system was programmed to move to the next loading step 30 min after the end of primary consolidation. Primary consolidation is defined as the period over which the change in specimen height is associated solely with the dissipation of pore water pressure, whereas secondary consolidation is defined as strain associated with the realignment of particles within the sediment matrix (Terzaghi, 1943; Sridharan and Rao, 1982). The most reliable method for assessing the end of primary consolidation (EOP) is through the measurement of pore pressures during loading and settlement; however, the EOP can also be reliably determined by analyzing the time deformation data during settlement. No pore pressure measurements were performed during testing, and for all tests, the EOP was determined by analyzing the time deformation data using Taylor's (1948) square root of time method.
Along the virgin compression curve, where permeability measurements were acquired, secondary consolidation was allowed to progress until permeability tests were completed; typically this was ~24 hr, but in some instances where the permeability was exceptionally low, testing took between 3 and 5 days.
On the lever arm system, samples were allowed to settle for 24 hr after the application of each new load. During loading and settlement, the change in specimen height was monitored using both a dial gauge and a digital displacement transducer connected to acquisition software. Similar to the Loadtrack tests, secondary consolidation was allowed to proceed during permeability tests.
Permeability (K) is an intrinsic property of the sediment matrix, whereas the rate of fluid flow through sediment is a function of both the intrinsic permeability and the physical properties of the flowing fluid. The rate of fluid flow is termed Darcy's coefficient of permeability, or hydraulic conductivity (k). The relationship between hydraulic conductivity and permeability is expressed by
-
K = k
 g/µ, (1)
g/µ, (1)
where
-
K = intrinsic permeability (L2),
-
k = hydraulic conductivity (L/T),
-
 = pore fluid density,
= pore fluid density,
-
g = gravitational acceleration, and
-
µ = fluid viscosity.
The hydraulic conductivity is reported here and normalized to seawater having a density of 1.024 g/cm3 at 20°C.
The flow of fluids through marine sediments plays an important role in regulating the temporal and spatial evolution of petrophysical properties. Information on the relationship between void ratio and permeability for a given sediment type are used to assess the role and impact of fluid flow. Void ratio-permeability relationships are derived from consolidation tests using Terzaghi's (1943) one-dimensional consolidation theory or measured directly using a low-gradient flow-pump technique at the end of each incremental load during testing. Terzaghi's derivation of permeability is calculated using
-
k = Cv
 g Av/(1 + e), (2)
g Av/(1 + e), (2)
where
-
k = hydraulic conductivity;
-
Cv = coefficient of consolidation, determined using either the curve fitting procedure of Taylor (1948) or Casagrande (1936) on the time deformation data during a given incremental load;
-
Av = slope of the load-displacement curve; and
-
e = average void ratio over the incremental load for which the hydraulic conductivity is being determined.
This theoretical derivation is based upon a number of nested assumptions. It requires that the sample be homogeneous and 100% saturated. The solids and the water in pore spaces are assumed to be incompressible, with drainage occurring solely from vertical compression. It requires that effective stress maintain a unique relationship with the void ratio of the sample, which implies that both the slope of the consolidation curve (Av) and Darcy's coefficient of permeability (hydraulic conductivity [k]) remain constant during any loading step. This condition of maintaining a unique relationship between effective stress and void ratio assumes that only primary consolidation occurs. Permeability estimates made using Terzaghi's one-dimensional theory tend to be slightly lower than actual permeability because secondary consolidation consistently plays a small role in the deformation of a sample under a load (MacKillop et al., 1995).
A more accurate way of determining hydraulic conductivity is through direct measurement using a low-gradient flow-pump technique. Recommendations for low-gradient testing of fine-grained sediments using a flexible-wall permeameter are outlined in ASTM designation D 5084-90 (ASTM International, 1990). The same testing procedures can be applied using a consolidation cell. Flow pump tests were conducted at the end of primary consolidation at each step along the virgin compression curve for selected samples. Constant rate of flow tests apply a known flow rate (q) through a sample. This flow rate establishes a head difference across the sample that is monitored using a differential pore pressure transducer. When the head equilibrates, a steady-state gradient is established (i) and the hydraulic conductivity is calculated using Darcy's law:
-
q = k i A, (3)
where
-
q = known flow rate (L3/T),
-
k = hydraulic conductivity (L/T),
-
i = dimensionless hydraulic gradient (
 h/
h/ l), and
l), and
-
A = cross-sectional area of the sample (L2).
Terzaghi's theory was used here to calculate sediment permeability during loading along the virgin compression curve for each sample. Where hydraulic conductivities were large enough for direct measurements, complementary permeability measurements were made using a low-gradient flow-pump technique. During flow pump testing, three flow rates were attempted and applied in both directions across the sample, resulting in a maximum of six direct measurements of hydraulic conductivity at each void ratio. Because Darcy's law states that the hydraulic conductivity should be independent of flow rate, the slope of a q-i plot at a given void ratio should be linear. Nonlinearity is an indication that Darcy's law has been violated and the measurements are invalid. The slope of the q-i plot was used for each series of measurements to define the hydraulic conductivity of the sample at a particular void ratio. The regression of the q-i data was forced to pass through the origin because a hydraulic gradient does not exist when the flow is zero. An e-log(k) relationship, in the form of an exponential function, is presented for each sample. When flow pump measurements existed, these were used to define the relationship and are deemed more accurate than derived measurements. In the absence of flow pump measurements, the derived permeability data were used to calculate the e-log(k) relationship for that sample.
Effective stress is defined as the stress that is passed between particles in the sediment matrix and is calculated by removing the fluid pressure (u) from the lithostatic overburden, or total stress ( ):
):
-
 ´ =
´ =  – u. (4)
– u. (4)
If hydrostatic fluid pressures are assumed,  ´ can be directly calculated using bulk density data:
´ can be directly calculated using bulk density data:
-
 ´ = (
´ = ( s –
s –  w)hg, (5)
w)hg, (5)
where
-
 s = sediment bulk density,
s = sediment bulk density,
-
 w = density of seawater, and
w = density of seawater, and
-
h = burial depth.
The in situ effective stress was calculated using the index property–derived bulk density values and the composite depth scales generated on board the ship. No rebound correction was applied to the depth scales and calculations assume hydrostatic fluid pressures. The average bulk density was used to calculate the effective stress between consecutive downhole samples and rounded to the nearest 5 kPa.
The stress history of sediments is often described using the overconsolidation ratio (OCR), which is a ratio of Pc´ and the in situ  ´ under hydrostatic conditions (OCR = Pc´/
´ under hydrostatic conditions (OCR = Pc´/ ´). An OCR > 1 represents an overconsolidated sediment. Overconsolidation arises when an overburden pressure is removed from a consolidated sediment column. Such conditions arise, for example, with glacial loading and subsequent melting or lithologic loading with subsequent removal of sediment by erosion. An OCR
´). An OCR > 1 represents an overconsolidated sediment. Overconsolidation arises when an overburden pressure is removed from a consolidated sediment column. Such conditions arise, for example, with glacial loading and subsequent melting or lithologic loading with subsequent removal of sediment by erosion. An OCR 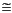 1 indicates that the sediment is normally consolidated, meaning the current in situ effective stress represents the maximum stress the sample has experienced. A normally consolidated state implies that hydrostatic fluid pressures are present in the sediment column. Sediments with an OCR < 1 are underconsolidated, a state which suggests the presence of excess pore pressures within the sediment column. Excess pore pressures develop through disequilibrium compaction associated with high sedimentation rates or the development of an overlying hydraulic seal, which impedes the dissipation of pore waters (Rubey and Hubbert, 1959; Fertl, 1976).
1 indicates that the sediment is normally consolidated, meaning the current in situ effective stress represents the maximum stress the sample has experienced. A normally consolidated state implies that hydrostatic fluid pressures are present in the sediment column. Sediments with an OCR < 1 are underconsolidated, a state which suggests the presence of excess pore pressures within the sediment column. Excess pore pressures develop through disequilibrium compaction associated with high sedimentation rates or the development of an overlying hydraulic seal, which impedes the dissipation of pore waters (Rubey and Hubbert, 1959; Fertl, 1976).
By definition, the OCR is a more sensitive indicator of stress state in near-surface sediments when compared with deeply buried formations. In shallowly buried sediments where  ´ < 500 kPa, uncertainties associated with sample disturbance and effective stress calculations can have significant impacts on the calculated OCR. Because of this uncertainty, Dadey and Silva (1989) used OCR
´ < 500 kPa, uncertainties associated with sample disturbance and effective stress calculations can have significant impacts on the calculated OCR. Because of this uncertainty, Dadey and Silva (1989) used OCR 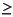 1.2 to represent overconsolidation and OCR
1.2 to represent overconsolidation and OCR 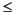 0.7 for underconsolidation. As the depth of burial increases, a greater offset between Pc´ and the in situ
0.7 for underconsolidation. As the depth of burial increases, a greater offset between Pc´ and the in situ  ´ is required for a significant OCR ratio to develop. Furthermore, the accuracy in the evaluation of Pc´ decreases at higher effective stresses because it is determined using a curve-fitting method on a log-linear plot.
´ is required for a significant OCR ratio to develop. Furthermore, the accuracy in the evaluation of Pc´ decreases at higher effective stresses because it is determined using a curve-fitting method on a log-linear plot.
During sample preparation, an ~30 g subsample was used to determine the void ratio of test specimens prior to consolidation by measuring wet and dry mass. Drying was performed at 105°C over a period of 24 hr. The salt-corrected water content was calculated from the wet and dry mass of the subsample using
-
w = (Mwet – Mdry)/[Mdry – (0.035Mwet)], (6)
where
-
w = water content (%),
-
Mwet = wet mass of the subsample (g), and
-
Mdry = dry mass of the sample.
The calculated water content was used to determine the mass of solids and liquid within the test sample:
-
Msolid = Msample/[1 + (w/100)] and (7)
-
Mwater = Msample – Msolid. (8)
Using the specific gravity (Gs) of the sample, the volume of solids (Vs), water (Vw), and air (Va) were determined:
-
Vs = Msolid/Gs, (9)
-
Vw = Mwater/1.024 g/cm3, and (10)
-
Va = VT – Vs – Vw , (11)
where VT is the total sample volume calculated from its height and diameter.
Specific gravity was either measured directly in the laboratory or derived from shipboard measurements of grain density. When derived from shipboard moisture and density data, the average grain density for the entire core was used. The void ratio of the sample is defined as
-
e = Vv/VT , (12)
where
-
Vv = Va + Vw and (13)
-
VT = Va + Vs + Vw . (14)
The calculated void ratio was used to define the void ratio of the test specimen prior to testing. For the two black shale samples (Samples 207-1257C-13R-1, 140 cm, and 207-1258B-45R-4, 45 cm), residues from oven drying at 105°C were weighed before heating to 550°C for 1 hr. This allowed the total organic carbon (TOC) content to be determined using a loss on ignition approach:
-
%org = (M100 – M550)/M100, (15)
where
-
%org = total organic content,
-
M100 = mass of the sample after drying at 100°C,
-
M550 = mass of the sample after drying at 550°C, and
-
TOC = %org x 0.44, (16)
where 0.44 represents an approximate contribution of organic carbon to the molecular weight of organic material by assuming a cellulose composition.

 ´) and allowing the pore pressure to dissipate as the sediment settles. The change in sample height under each new load is used to calculate the volumetric strain or void ratio (e) at the end of each step and defines the sediment's compressibility. Because soils are not perfectly elastic, the deformation behavior they exhibit depends on the stress history of the sample. This allows four critical parameters to be derived from a consolidation test:
´) and allowing the pore pressure to dissipate as the sediment settles. The change in sample height under each new load is used to calculate the volumetric strain or void ratio (e) at the end of each step and defines the sediment's compressibility. Because soils are not perfectly elastic, the deformation behavior they exhibit depends on the stress history of the sample. This allows four critical parameters to be derived from a consolidation test:
 g/µ, (1)
g/µ, (1)
 h/
h/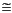 1 indicates that the sediment is normally consolidated, meaning the current in situ effective stress represents the maximum stress the sample has experienced. A normally consolidated state implies that hydrostatic fluid pressures are present in the sediment column. Sediments with an OCR < 1 are underconsolidated, a state which suggests the presence of excess pore pressures within the sediment column. Excess pore pressures develop through disequilibrium compaction associated with high sedimentation rates or the development of an overlying hydraulic seal, which impedes the dissipation of pore waters (Rubey and Hubbert, 1959; Fertl, 1976).
1 indicates that the sediment is normally consolidated, meaning the current in situ effective stress represents the maximum stress the sample has experienced. A normally consolidated state implies that hydrostatic fluid pressures are present in the sediment column. Sediments with an OCR < 1 are underconsolidated, a state which suggests the presence of excess pore pressures within the sediment column. Excess pore pressures develop through disequilibrium compaction associated with high sedimentation rates or the development of an overlying hydraulic seal, which impedes the dissipation of pore waters (Rubey and Hubbert, 1959; Fertl, 1976).
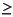 1.2 to represent overconsolidation and OCR
1.2 to represent overconsolidation and OCR 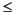 0.7 for underconsolidation. As the depth of burial increases, a greater offset between Pc´ and the in situ
0.7 for underconsolidation. As the depth of burial increases, a greater offset between Pc´ and the in situ