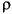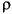1 and 2 and velocities v1 and v2 is given for vertical incidence waves by the Zoepritz equation:
Meteor Cruise M 49/1 in early 2001 from Cape Town (South Africa) to Montevideo (Uruguay) was the main presite survey for Leg 208. The main objectives were to collect high-resolution seismic reflection profiles to identify drill sites that promise recovery of undisturbed, complete, and possibly expanded Paleogene sequences in different water depths. Seismic profiles with a total length of ~1800 were acquired in the study area in water depths between ~2.5 and 4.5 km (Fig. F1).
The multichannel seismic system of the University of Bremen is specifically designed to collect seismic data with high lateral and vertical resolution. The alternating operation of a small-chamber water gun (0.16 L; 200–1600 Hz), a generator-injector (GI) gun with reduced chamber volume (0.4 L; 100–500 Hz), and a GI gun with normal chamber volume (1.7 L; 30–200 Hz) yielded three seismic data sets simultaneously. For recording of the GI gun and water gun data, a 96-channel Syntron streamer 600 m in length and equipped with separately programmable hydrophone groups was used. In this manuscript, we will only present GI gun data. A total of 48 channels consisting of 13 hydrophones each, a group length of 6.25 m, and a group distance of 12.5 m were used for recording GI gun data. The shot interval was 9 s, resulting in a shot distance of ~25 m when sailing with an average speed of 6 kt. Ten birds kept the streamer at a constant water depth of ~3 m below the sea surface within a range of 1 m. A magnetic compass at every bird allowed determination of hydrophone group position relative to the ship's course. GI gun data were digitally recorded at a sampling frequency of 4 kHz over a record length of 3000 ms. Positioning was based on Global Positioning System (GPS). For processing of seismic data a combination of in-house and commercial (Vista) software (Seismic Image Software LTD) was used. Standard seismic processing procedures employed included trace editing, setting up geometry, static and delay corrections, velocity analysis, normal move-out (NMO) corrections, bandpass frequency filtering, stacking, and time migration. A common midpoint (CMP) distance of 10 m was chosen for processing.
The reflection coefficient (R) between media of densities 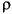1 and 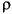2 and velocities v1 and v2 is given for vertical incidence waves by the Zoepritz equation:
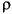1 · v1) – (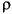2 · v2)]/[(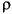1 · v1) + (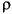2 · v2)].
The sequence of velocity and density changes with depth below the seafloor is referred to as Earth's reflection coefficient series. This series can be transformed into two-way traveltime (TWT) scale using velocity measurements. The synthetic seismogram can be calculated by mathematically convolving this series with the seismic wavelet. The impulse response function for seismic modeling was computed using the state space approach (Mendel et al., 1979), which also takes all possible internal reflections into account. By comparing reflectors in the synthetic seismogram with core density measurements, it is possible to assign reflectors to geologic events. The detailed procedure for calculating the synthetic seismogram is described below.
GRA density measurements with a sampling interval of 2 to 3 cm are available for all Leg 208 sites. All sites consist of two to four holes. As individual holes usually do not recover the entire stratigraphy of a site, it is necessary to merge and edit the density data to create composite data sets for each site (Fig. F2A, F2B). This was done using stratigraphic tie points determined during the cruise (Shipboard Scientific Party, 2003).
After creating a composite data set for each site, a moving window with a length of 50 measured values was used to calculate a local average density and to detect spurious density values, likely caused by voids, cracks, or gas bubbles within the cores and at the ends of the core sections. These artifacts cause unrealistic values for reflection coefficients and thus are replaced by the last density value accepted by the moving window. The criterion to replace was that a value should not differ more than four times the root mean square deviation of the window. Furthermore, data gaps that could not be filled were linearly interpolated to avoid unnatural reflection coefficients caused by small data gaps. A correction of the GRA density values to in situ conditions, which accounts for decrease in hydrostatic pressure, temperature change, and porosity rebound during core recovery (Hamilton, 1976), was not carried out because relative density variations especially for the upper 150 m of the sediment column will not be significantly changed (e.g., Mosher et al., 1993; Rohr and Gröschel-Becker, 1994).
Sampling intervals of whole-core velocity data sets are ~25 cm and more, which is much larger than the sampling intervals of the GRA density measurements of Leg 208 cores (Shipboard Scientific Party, 2003). This discrepancy makes it impossible to calculate reflection coefficients with a detailed velocity model. Additionally, detailed velocity measurements were not done at all depths of each site. Adventitious velocity data are less important for the calculation of reflection coefficients because values scatter around a mean trend and variations in marine surface sediments do not exceed 5% (e.g., Weber et al., 1997; Breitzke, 2000). In contrast, associated density variations within marine surface sediments are usually >20% (e.g., Weber et al., 1997; Breitzke, 2000). A careful analysis of velocity and GRA density measurements shows a positive correlation of smaller velocity excursions and density variations. Therefore, the effect of the velocity data on the reflection coefficient is small. We estimate the overall error, which is introduced by assuming a smooth velocity depth profile and ignoring the velocity contribution to variations in reflection coefficients, to be only 10%–20%. Zühlsdorff and Spiess (2001) estimated similar errors using the same methods for data from ODP Leg 168 at the eastern flank of Juan de Fuca Ridge.
Close inspection of velocity data also shows a large number of spurious data points. These facts support the use of a simple velocity model that is still sufficient to identify our target reflectors but with obvious restrictions. For example, interpretation of waveforms, as well as interpretation of amplitudes of individual reflectors, is of limited quality because effects such as interference definitely cause discrepancies between recorded and modeled data.
The velocity model is, of course, also needed for conversion of the meters below seafloor scale to a timescale.
After creating whole continuous GRA density data sets for each site, it is necessary to convert the meters below seafloor scale to a timescale and to calculate the series of reflection coefficients. In the first step, a constant velocity of 1500 m/s was used. A sampling interval of 250 µs, which is the same as for seismic data, was used to preserve complete information for GRA density measurements. To create a seismic trace, density data must be convolved using a seismic wavelet. Although it is possible to pick seafloor reflections, a synthetic wavelet is used. Synthetic wavelets are smoother than recorded wavelets and appear to be more useful for visual correlation of reflection patterns. Differences in vertical energy distribution between synthetic wavelets and recorded wavelets do not appear (Zühlsdorff and Spiess, 2001). In this study, for convolving reflection coefficients, a Ricker wavelet (Ricker, 1953) with a frequency of 150 Hz, which is the main frequency of the GI gun, was used (Fig. F2A, F2B, F2C, F2D). Synthetic data were then compared with seismic data at the CMP of the drill site location. In the next step, the velocity model was fine tuned using velocity information from whole-core analysis to improve depth to time conversion for better synthetic to seismic matching. It turned out that the best-fit velocity models usually correspond to linear regressions of velocity measurements, which take the general velocity trend into account, namely the increase of the velocity with depth, but neglect all small-scale velocity variations (Fig. F2A, F2B, F2C, F2D).
For Site 1267 no velocity measurements or information exist; therefore, a velocity model of a nearby drill site is used. In this case, the velocity model of Site 1266 is used; Site 1266 is located on the same seismic profile, GeoB01-030, which is characterized by only few changes in the sedimentation pattern.
