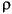 m -
m - 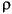 s)Ssed
/(
s)Ssed
/(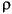 m -
m - 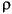 w),
w),
A primary objective of Leg 194 was to establish the magnitude of the middle Miocene (Zones N12-N14) sea level fall based on the expected stratigraphic relationships between the northern MP2 and the southern MP3 platforms. MP3 was believed to be nucleated on the distal slope sediments of MP2 during the maximum sea level lowstand. However, drilling results at Sites 1196 and 1199 showed that the southern platform is composed of ~120-160 m of MP3 platform overlying a middle to early Miocene platform. This stratigraphic architecture makes estimates of sea level variations difficult using the original proposed methodology. Nevertheless, sequence stratigraphic and facies relationships from the transect drilled across the northern platform, consisting of Sites 1193 and 1194, allow an estimate of the magnitude of the sea level fall to be made. The top of the platform at Site 1193 (35 mbsf) was deposited during the middle Miocene (~12-16 Ma) at an estimated paleowater depth of 10-50 m (Table T3) and represents the middle Miocene highstand. Lithologic Subunit IIIA at Site 1194 (117-154 mbsf), deposited during the latest middle Miocene (11-14 Ma), represents a shallow-water (30-50 m) interruption of a generally deeper water sedimentation environment. The base of Subunit IIIA today lies 145 m below the top of MP2 at Site 1193, and seismic correlation between the two sites suggests that Subunit IIIA was deposited after the platform top of MP2 was exposed (Fig. F13A). Consequently, these sequences provide a means to estimate the amount of sea level drop needed to move the shallow-water deposition environment from the top of MP2 at Site 1193 to the base of Subunit IIIA at Site 1194. Sediment and water loading that have occurred since the end of the middle Miocene compacted earlier deposited sediments and thus affected the sequence geometry. These effects need to be removed in order to estimate the magnitude of the sea level drop. This can be accomplished by using the sediment thickness and porosity data of the overlying and underlying sections, and the paleowater depth estimates at the times just before and after the sea level fall. In addition, local isostasy in response to sediment and water loading may have further affected the difference in elevation between the top of MP2 at Site 1193 and the base of Subunit IIIA at Site 1194. Isostatic correction is based on the density difference between the added water-sediment layers and an equivalent thickness of mantle at an assumed density of 3.3 g/cm3. Two end-member paleotopographic reconstructions are presented for extreme crustal response to sediment and water loading: (1) complete local isostasy (zero flexural strength in the basement) and (2) no differential subsidence (infinite flexural strength in the basement). Assuming local isostasy for the basement response to sediment and water loading and unloading, it is possible to reconstruct the present-day geography of the MP2 platform at Site 1193 with respect to the downlap surface produced by the shedding of material from the platform (Fig. F13; lower reflection marked by arrow; lithologic Subunit IIIA). The present-day water depth at Site 1193 in the absence of sediment can be calculated using
where Swater is the water depth after the removal of the sediment from the MP2 platform and Ssed is the sediment thickness on top of the MP2 platform at Site 1193 (35 m) or on top of Subunit IIIA at Site 1194 (154 m). In addition,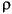 m,
m,
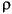 w, and
w, and 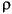 s are the mantle, water, and average
sediment densities, respectively (Table T3). Present-day bathymetries at Site 1193 and 1194 are 348 and 374 m.
Applying the above equation, the calculated Swater
for Sites 1193 and 1194 is 25 m and 106 m, respectively, giving a reconstructed present-day water
depth in the absence of sediment, Wd, of
374 and 480 mbsl (Fig. F13B).
s are the mantle, water, and average
sediment densities, respectively (Table T3). Present-day bathymetries at Site 1193 and 1194 are 348 and 374 m.
Applying the above equation, the calculated Swater
for Sites 1193 and 1194 is 25 m and 106 m, respectively, giving a reconstructed present-day water
depth in the absence of sediment, Wd, of
374 and 480 mbsl (Fig. F13B).However, as sediment is removed, the thickness of the underlying sediments must be adjusted to reflect the original, decompacted state of the sediment. The measure of compaction is sediment porosity, which was measured at both sites. Porosity (f) can be related to depth (z) using an exponential function and a porosity decay parameter (k) such that
A least-squares fit of
this function to Site 1194 porosity data yields f0 = 65% and k = 0.002/m (correlation coefficient =
0.91). This normal compaction trend suggests hydrostatic fluid pressures were maintained during the
deposition and compaction process and that the equation above can be used to simulate the compaction
(and decompaction) of the sediment column. Removing lithologic Units I, II, and IIIA (a total
thickness of 154 m) induces 56 m of decompaction. Porosity at Site 1193 shows a general decrease with
depth, except within the platform sediments, where values are scattered, ranging from 10% to 45%,
reflecting the various degrees of cementation in the carbonate rocks. Ignoring the porosity interval
spanned by the cemented platform, the equivalent least-squares fit for Site 1193 porosity data yields
f0 =
61.2% and k = 0.001/m (correlation coefficient = 0.60). Removing lithologic Units I and II (a total
thickness of 35 m), expansion of the sediment packages below the cemented carbonate platform induce 7
m of decompaction. The corrected water depths for the late middle Miocene stratigraphic Sites 1193 and
1194 are therefore 367 and 424 m, respectively. We now have to reconstruct the water depth at the time
of the middle Miocene highstand from the reconstructed present-day water depths. As we reduce the
water column, the basement and overlying sediments are unloaded and so will flexurally rebound. The
following equation determines the sea level change (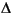 SL) responsible for producing a given paleowater depth (Swater) including the isostatic adjustment of the basement associated
with the sea level change
SL) responsible for producing a given paleowater depth (Swater) including the isostatic adjustment of the basement associated
with the sea level change
Considering the estimated 10-50 m paleowater depth at Site 1193 during the middle Miocene highstand, sea level must be decreased by 219-246 m (Fig. F13B). The water-depth at Site 1194 at NP12 time is given by the reconstructed water depth of 424 m minus the DSL change of 219-246 m minus the isostatic adjustment (rebound) induced by this sea level change, given by
Evaluating gives a rebound range of 98-110 m. The corresponding highstand water-depth at Site 1194 is thus 67-107 m. From this time on, sea level falls. At the time of the maximum lowstand, the paleowater depth at Site 1194 is estimated from paleontological assemblages to be 30-50 m. The sea level drop required is therefore 12-53 m (Fig. F13C).
The assumption of local isostasy minimizes the estimated eustatic fall. Given the undisturbed and consistently dipping sediments, the relative small distance (~20 km) between Sites 1193 and 1194, as well as the horizontal basement geometry between the sites, suggests that no significant differential subsidence occurred between them. If we assume the other end-member model of infinite flexural strength of the lithosphere, the present-day geometry between Sites 1193 and 1194 is maintained except for the decompaction. The total water depths at Sites 1193 and 1194 without overlying sediment and including the effects on decompaction are 376 and 472 m, respectively. The geometric relief between the platform and Site 1194 is thus 145 m. Given the paleowater depth estimates at Sites 1193 and 1194 of 10-50 m and 30-50 m, respectively, the corresponding range in the estimated eustatic fall is 56-116 m. Thus, an extremely conservative estimate of the NP12-NP14 middle Miocene eustatic fall based on Leg 194 drilling, considering both the effects of sediment compaction and the range in flexural behavior of the lithosphere, is 64-52 m. However, given the much more reasonable scenario of finite flexural strength of the lithosphere, our best estimate of the eustatic fall is 86-30 m. Platform erosion at Site 1193 and overall tectonic subsidence during the sea level lowering were not considered. Both effects are much smaller than the error margin and would increase the sea level fall. It is also possible that a record of the lowest sea level was not preserved, cored, or observed in Subunit IIIA at Site 1194, which would also increase the magnitude of the eustatic fall.