-
 , (1)
, (1)
In sedimentary basins, the porosity of the sediment decreases in a regular fashion with depth as long as the pore fluid remains hydrostatic. The relationship between porosity and effective stress variations is derived in the following manner. We define a long-term porosity compressibility by:
where  is the total interconnected porosity,
is the total interconnected porosity,  O is the porosity in an uncompacted reference state corresponding to the seafloor in sedimentary basins,
O is the porosity in an uncompacted reference state corresponding to the seafloor in sedimentary basins,  eff =
eff = - p,
- p,  is the total confining stress, which is the first invariant of the total stress tensor, and p is the total fluid pressure (equal to the hydrostatic fluid pressure, pH, plus a fluid overpressure term,
is the total confining stress, which is the first invariant of the total stress tensor, and p is the total fluid pressure (equal to the hydrostatic fluid pressure, pH, plus a fluid overpressure term,  p). Palciauskas and Domenico (1989) show that compaction by pressure solution in sedimentary basins is irreversible and several orders of magnitude more effective than the corresponding poro-elastic (reversible) compressibility. They also show theoretically that
p). Palciauskas and Domenico (1989) show that compaction by pressure solution in sedimentary basins is irreversible and several orders of magnitude more effective than the corresponding poro-elastic (reversible) compressibility. They also show theoretically that  does not depend on the effective stress itself. We can recast Equation 1 in the following form:
does not depend on the effective stress itself. We can recast Equation 1 in the following form:
where  will be considered as a constant as shown by Palciauskas and Domenico (1989). In the following, we will consider
will be considered as a constant as shown by Palciauskas and Domenico (1989). In the following, we will consider  eff
eff 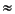 (P - p) where P is the lithostatic stress. This approximation is valid only in absence of strong tectonic stresses, and with a Poisson's ratio close to 0.50 (Magara, 1978). The Poisson ratio for long-term deformation of mud or unconsolidated sediments such as observed at the sites investigated is close to 0.50 (Hamilton, 1971). The change in lithostatic and fluid pressures under hydrostatic conditions (subscript H) over a depth increment dz are given by (Magara, 1978):
(P - p) where P is the lithostatic stress. This approximation is valid only in absence of strong tectonic stresses, and with a Poisson's ratio close to 0.50 (Magara, 1978). The Poisson ratio for long-term deformation of mud or unconsolidated sediments such as observed at the sites investigated is close to 0.50 (Hamilton, 1971). The change in lithostatic and fluid pressures under hydrostatic conditions (subscript H) over a depth increment dz are given by (Magara, 1978):
where  H is the "hydrostatic porosity" (Fig. 2),
H is the "hydrostatic porosity" (Fig. 2),  f is the density of the fluid in the interconnected pore space,
f is the density of the fluid in the interconnected pore space,  m is the grain density, and g is acceleration of gravity. In the presence of gas, the fluid density
m is the grain density, and g is acceleration of gravity. In the presence of gas, the fluid density  f can be related to the water saturation Sw, and to the gas density
f can be related to the water saturation Sw, and to the gas density  g by
g by  f = Sw
f = Sw w + (1-Sw)
w + (1-Sw) g where
g where  w is the saline water density. Because, the differential of the effective stress is given by d
w is the saline water density. Because, the differential of the effective stress is given by d eff
eff 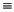 d
d - dp = dPH - dpH, Equations 3 and 4 allow the compaction equation, Equation 2, to be rewritten:
- dp = dPH - dpH, Equations 3 and 4 allow the compaction equation, Equation 2, to be rewritten:
Integration from the seafloor (z = 0,  =
=  0) to depth z yields:
0) to depth z yields:
where the characteristic depth zc is defined by:
Equation 6 can be rewritten to give:
Equation 8 corresponds to the normal trend of compaction in sedimentary basins. Finally, the lithostatic pressure in a hydrostatically pressured section, PH, can be obtained by substituting Equation 8 into Equation 3 and integrating from the surface to the depth z, yielding:
Fluid overpressure is the result of a balance between the rate of overpressure generation and its dissipation by fluid flow (Palciauskas and Domenico, 1989). In this paper, we only consider fluid overpressures resulting from disequilibrium compaction. Disequilibrium compaction refers to the situation where sediments are unable to expel their pore fluids in response to sediment loading, which causes fluid overpressure. It is convenient to describe all parameters as departures from the values these parameters would have under hydrostatic conditions. Defining the departure from hydrostatic pore pressure, lithostatic pressure, and porosity by  p,
p,  P, and
P, and 
 , we can write the fluid pressure, the lithostatic pressure, and the porosity without loss of accuracy:
, we can write the fluid pressure, the lithostatic pressure, and the porosity without loss of accuracy:
where pH =  fgz is the hydrostatic fluid pressure, and PH and
fgz is the hydrostatic fluid pressure, and PH and  H are given by Equations 8 and 9, respectively. We call
H are given by Equations 8 and 9, respectively. We call 
 the "excess porosity" (Fig. 2). From Equations 2, 10, 11, and 12, the porosity change
the "excess porosity" (Fig. 2). From Equations 2, 10, 11, and 12, the porosity change 
 is related to the effective stress change,
is related to the effective stress change,  P -
P -  p, by:
p, by:
The lithostatic stress is related to the porosity by:
Combining Equations 3, 11, 12, and 14, we have:
 . (15)
. (15)
Combining Equations 13 and 15, we see the excess fluid pressure and the excess porosity are related by:
or alternatively, using the definition of the characteristic depth zc, Equation 7,
 . (17)
. (17)
The second term of Equation 17 represents the variation of the lithostatic pressure induced by variations of the excess porosity 
 . Equations 13-17 are exact in the sense that they do not result from any approximation other than the constraint of disequilibrium compaction discussed above. Provided
. Equations 13-17 are exact in the sense that they do not result from any approximation other than the constraint of disequilibrium compaction discussed above. Provided  p
p 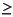 0,
0, 
 is necessarily positive.
is necessarily positive.
Lithologic variations and, in particular, the compaction of sediments in which clay minerals mix with sand grains can be quantified for sand/shale mixtures as illustrated in Figure 3. The noncompacted porosity is obtained from the clay weight fraction, 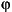 W, by:
W, by:
 , (18)
, (18)
where  Sd and
Sd and  Sh (
Sh ( Sd and
Sd and  Sh) are respectively the interconnected porosity (the grain density) for a noncompacted clean sand and a noncompacted pure shale. The critical shale content
Sh) are respectively the interconnected porosity (the grain density) for a noncompacted clean sand and a noncompacted pure shale. The critical shale content
![]() , which characterizes the boundary between the clayey sand domain and the sandy shale domain (Fig. 3), is defined by:
, which characterizes the boundary between the clayey sand domain and the sandy shale domain (Fig. 3), is defined by:
It follows from Equations 8, 18, and 19 that the porosity can be predicted completely from the knowledge of the shale content of the formations, the depth, the uncompacted porosity  0, and the compressibility
0, and the compressibility  . The uncompacted porosity and the compressibility are determined in the upper section of the sedimentary column provided that this domain is hydrostatically pressured.
. The uncompacted porosity and the compressibility are determined in the upper section of the sedimentary column provided that this domain is hydrostatically pressured.
The gamma-ray log is a measure of the natural radioactivity of the sediment formations, and can be used to estimate the shale content (Ellis, 1987). We assume that the clay weight fraction of the formations is given to a first order by:
where 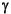 is the gamma-ray reading,
is the gamma-ray reading, 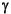 Sd is the gamma-ray value of a pure sand, assumed here to be equal to ten gamma-ray units, whereas
Sd is the gamma-ray value of a pure sand, assumed here to be equal to ten gamma-ray units, whereas 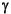 Sh is the gamma-ray value of a pure shale (120 gamma-ray units). This equation should be considered as a rough approximation because (1) nonradioactive clay minerals may be present, and (2) uranium-rich formations can be interpreted as shale layers (Ellis, 1987). We assume the following:
Sh is the gamma-ray value of a pure shale (120 gamma-ray units). This equation should be considered as a rough approximation because (1) nonradioactive clay minerals may be present, and (2) uranium-rich formations can be interpreted as shale layers (Ellis, 1987). We assume the following:  m =
m =  Sh =
Sh =  Sd = 2650 kg m-3, and
Sd = 2650 kg m-3, and  Sd =
Sd =  Sh = 0.65.
Sh = 0.65.