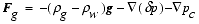DISCUSSION

The high compressibility inferred from the data is probably a result of two phenomena: (1) mechanical compaction, which is usually the dominant deformation mechanism at shallow depths, and (2) compaction by pressure solution. A. Revil and L.M. Cathles (unpubl. data) reported that high geothermal gradients increase the compaction coefficient associated with pressure solution in sedimentary basins. Precipitation of high-magnesium calcite here seems to be indicated, for example, at Site 977 from magnesium and calcium concentration profiles with depth (Shipboard Scientific Party, 1996c). Authigenic calcite rhombs were observed in Cores 161-977A-2H, 3H, and 4H. Biogenic carbonate recrystallization releases strontium to the pore space (Deer et al., 1966). Carbonate recrystallization at depth is suggested by the increase in strontium concentrations from ~100 µM in the top 37 m to 1437 µM at 477.7 mbsf at Site 977. Similar variations are also reported at other sites drilled during Leg 161. However, the amount of recrystallized carbonate is not significant enough to seal fluids by decreasing the intrinsic permeability of the formations. The large fluid overpressures observed in all holes inhibit, or, at least, slow down dissolution/reprecipitation processes by pressure solution. In the presence of high fluid pressures in the pore space, load is transferred from the grain-to-grain contacts to the fluid phase (Palciauskas and Domenico, 1989).

The observed fluid overpressures could result from disequilibrium compaction associated with the high sedimentation rates recorded in these areas (50-200 m/m.y.). The sedimentary columns analyzed form layered systems and vertical permeability is limited by the permeability of the shaly layers. However, to explain the observed fluid overpressures, the permeability should be ~1 nD. The sediments observed are not very compacted, not very cemented, and not very shaly, as shown by the gamma-ray log. Their permeability is likely to be >1 mD. Even if relative permeabilities are considered because of the presence of free gas, a permeability of 1 nD would be difficult to obtain for these poorly compacted sediments. Consequently, another mechanism may be inhibiting vertical flow at the sites investigated and is responsible for the maintenance of the observed fluid overpressures.

In the case of a two-phase flow perpendicular to stratified formations consisting of alternating fine/coarse grained sediments, capillary effects can seriously affect the flow of both phases (Berg, 1975; Lenormand et al., 1994). Capillary blockage is well known in soil sciences (Ross, 1990; Steenhuis et al., 1991). A capillary seal is formed when the gradient of the capillary pressure (a function of the surface tension between water, the wetting fluid for the mineral grains, and gas, the nonwetting fluid) is greater or equal than the fluid overpressure of water (Fowler, 1970). In the presence of free gas, capillary pressure drops are formed at each interface between sediments of different grain sizes. Contacts between sand- or silt-rich layers and the clay-rich sediment such as observed at many sites and the presence of free methane can generate capillary pressure drops.

Sedimentation creates a compaction source term for the fluid overpressuring (Palciauskas and Domenico, 1989). The water overpressure drives an upward hydraulic two-phase flow. Gas is segregated in the sandy formations. The force applied to the gas, which is given by the following (England et al., 1987):

, (29)

where p_c is the capillary pressure. The capillary pressure is given by the Young-Laplace equation: p_c = (2/r)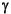 K where 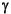is the interfacial tension of the gas-water interface (~72 x 10^-3 Nm^-1 at 25°C), r is a characteristic length scale that can be interpreted as an effective pore radius for transport in the interconnected pore space, and K is the "wetting coefficient" usually considered equal to unity. If the formations are perfectly homogeneous, dp_c /dz = 0. Where there are contrasts in grain size, a differential capillary pressure arises (Berg, 1975), which is given by:

p_c = 2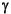 (1/r₂ - 1/r₁), (30)

where r₁ and r₂ are the two effective pore radius in the two formations in contact. Gas saturation increases with time at each fine/coarse interface contact. The saturation of gas in the coarse grain formations increases until it reaches such a high value that the gas phase become an interconnected phase (a "gas cap"). When this "critical state" is reached, water cannot flow, and the overpressure increases as more sediments are added to the sedimentary column. The water pressures must exceed the differential capillary pressure and push gas from the coarse to the finest grain-size formations (drainage) before any excess pressure can be dissipated. This is possible only if the fluid overpressure exceed the sum of the capillary pressure drops over the series of interfaces (i.e., the total capillary entry pressure; J. Shosa and L.M. Cathles, unpubl. data). To account for capillary sealing, the Darcy equation must be modified:

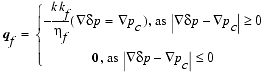, (31)

where q_f is the Darcy velocity, 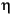_f is the dynamic shear viscosity of the fluid, p_c is the capillary pressure, k is the intrinsic permeability, and k_f (0 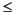k_f 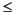1) is the relative permeability for water, which is a function of the water saturation (Rothman, 1990). Equation 31 is also similar to the equation obtained by Rothman (1990), derived for a two-phase flow in a channel of constant cross section. Equation 31 is supported by numerical and theoretical works (Lenormand et al., 1988; Rothman, 1990) and experimental works (J. Shosa and L.M. Cathles, unpubl. data). Equation 30 shows that the maximum fluid overpressure that a capillary seal (i.e., a permeability barrier associated with sand-shale interfaces in presence of gas caps) can support is equal to the sum of all the capillary pressure differentials inside the seal. We can replace the term ( ) in Equation 31 by (f p_c e), where f is the frequency of sand/shale interface which form the capillary seal, e is a local unit vector perpendicular to the interfaces and in the direction of the gradient of the capillary pressure, and p_c is the capillary pressure drop at each interface. A "normal flow" can only be re-established if the excess fluid pressure below the seal exceeds the total capillary entry pressure of the seal (f p_c), or if the fracture limit is reached.

At the contact between a clean sand and a clayey sand, a sandy shale, or a shale, the capillary entry pressure is given by (Berg, 1975):

, (32)

where r_fine and r_coarse are respectively the characteristic length scales for transport in the interconnected pore space of the fine and coarse grain-size sediments. These length scales can be related to more conventional geometrical parameters by (Revil et al., 1997):

, (33)

where d is an average grain diameter and m is the electrical cementation exponent, m 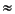1.6 ± 0.2 for clean sands, and 2.5 ± 0.3 for shales (Revil et al., 1997). Because the specific surface area of an equivalent granular porous media is given by V_p / S = (1/6) d / (1-), we can estimate an equivalent grain diameter from the specific surface area data of Patchett (1975) for the different clay minerals. We find the following: kaolinite: d = 1 µm, illite: d = 0.1 µm, and smectite: d = 1.10^-2 µm. Taking = 0.50, and the previous values for the grains diameters, the capillary entry pressures for the different clay minerals are the following: kaolinite: p_c = 1 MPa, illite: p_c = 10 MPa, and smectite: p_c= 100 MPa. These values are significant, and consequently capillary sealing could be a very efficient sealing mechanism in sedimentary basins regardless of the value of the intrinsic permeability of the sediments. Equations 32 and 33 can also have been tested using the laboratory experiments of J. Shosa and L.M. Cathles (unpubl. data), who measured experimentally the capillary entry pressure of two artificial sands with very narrow grain-size distributions (2 and 45 µm, porosity 0.45). They found p_c = 0.241 MPa per interface. The application of Equations 32 and 33 leads to p_c = 0.237 MPa, which shows, therefore, a very good agreement between theory and experiments.

Methane was present at all of the sites analyzed. Propane, iso-butane, and iso-pentane are also present in some formations (for example, between 200 and 450 mbsf at Site 977). At all sites, the origin of most of the methane seems to be biogenic, as indicated by on board headspace gas analysis (Comas, Zahn, Klaus, et al., 1996). We assume that the variation in amount of methane from one hole to another is probably controlled by the concentration of interstitial sulfate, which inhibits methanogenesis in marine sediments (Claypool and Kvenvolden, 1983). For example, at Sites 977 and 979, a biogenic origin of methane is supported by the disappearance of interstitial sulfate at the same depth at which methane concentration begins to rise. High sedimentation rates ensure that organic matter is buried more rapidly than dissolved oxygen can penetrate the sediments from the overlying seawater. In this case, only minor oxic and suboxic degradation of the organic matter occurs, hence fairly reactive organic matter would be preserved. After the sulfate is depleted, methanogenic bacteria degrades the organic matter, producing methane. Consequently, the intensity and depths range of methanogenesis and the sedimentation rate are related. At Sites 979 and 976, the depths of sulfate depletion are 25 mbsf and 24 mbsf, respectively (the sedimentation rates are ~200 m/m.y. and 210 m/m.y., respectively), and, in both cases, the concentrations of headspace methane are high. At Site 977, the depth of depletion of sulfate is 46.45 mbsf (the average sedimentation rate is ~135 m/m.y. until an unconformity located at ~500 mbsf in Hole 977A is reached), and the total headspace methane concentration is high. At Sites 974 and 975, for which the sedimentation rates are low (<100 m/m.y.; Fig. 7A, Fig. 7B), the overall methane concentration is low (Shipboard Scientific Party, 1996a, 1996b). The interstitial water-sulfate concentrations at these sites indicate that organic-matter degradation occurs mainly by sulfate reduction.

Watts (1987) described two types of capillary seals on the basis of their leaking mechanism. A membrane seal periodically leaks whenever the pore-fluid pressure differential across the seal exceeds the total capillary entry pressure of the seal allowing fluids to enter and pass through the finest grain sized sediments of the seal. Resealing occurs when the pore-fluid pressure drops below the capillary entry pressure. In the second case, a "hydraulic seal" is formed when the capillary entry pressure is so high that the pore-fluid pressure gradient necessary for fracturing the seal is less than the gradient needed to displace the nonwetting phase through the seal. These two types of capillary seals could explain why fixed and migrating seals are commonly observed in sedimentary basins (A. Revil and L.M. Cathles, unpubl. data). A fixed seal is defined as a permeability barrier attached spatially to a stratigraphic layer during the evolution of a sedimentary basin. A migrating seal is defined as a compartment that migrates in a framework attached to the stratigraphic layers. A complete theory of the dynamics of sealing is investigated by A. Revil and L.M. Cathles (unpubl. data).

In Hole 975C, an increase of porosity is observed below 170 mbsf. Because porosity variations in sedimentary basins are largely irreversible (Palciauskas and Domenico, 1989), this increase of porosity can be only explained as a "frozen porosity" because of the presence of a fixed seal between 145 and 170 mbsf. The presence of this fixed seal is correlated with small-scale lithologic variations in shale content in the same depth range as indicated by the gamma-ray log (Fig. 7A; gamma-ray log). This seal can be classified as a hydraulic seal because the fracture limit for unconsolidated sediment is reached (i.e., zero effective stress). Consequently, the fluid overpressures observed in Hole 975C could be the result of hydraulic seal with a cumulative capillary entry pressure >1.4 MPa (Fig. 7A; fluid overpressure curve) located between 145 and 170 mbsf. About ten layers containing gas are observed at the seal position, which would mean a capillary entry pressure >0.14 MPa per interface, easily obtainable for sediments with the observed sand/shale variations. This seal would have been formed at very shallow depth (below 30 mbsf), as indicated by the magnitude of the "frozen" porosity just below the seal (i.e., at 170 mbsf), in a period of high sedimentation rate (a high sedimentation rate is needed to produce methane at shallow depths, and is observed in Fig. 1 at the depth corresponding to the top of undercompaction, 154-178 mbsf).

In all the other holes analyzed, the porosity trend in the undercompacted formations is nearly a constant. This is typical of a migrating seal because the uniform porosity in these compartments requires a constant effective stress (porosity is a linear function of the effective stress, see Eq. 3). Consequently, the downward increase in pore-fluid overpressure is balanced by the downward increase in lithostatic load. This is possible only if the depth of the migrating seal remains fairly constant (i.e., the migrating seal moves in a framework attached to the geological formation sediments). In this case, there is a dynamic equilibrium between capillary and fluid overpressure forces of the seals that is maintained at the same depth over time. Sealing in these holes can be classified as membrane seal. It is striking to observe that the depth corresponding to the top of the overpressured section is always in the range 100-120 mbsf (except at Site 975 where a fixed seal is observed). This depth could be related to the bubble point of methane. The stability and the thermodynamic properties of methane in sedimentary basins are discussed by Brown (1990, and references therein).