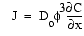CALCULATIONS AND MODEL RESULTS

Sulfate Flux

The flux of sulfate into the sediment from overlying seawater can be approximated from linear sulfate gradients using Fick's First Law:

  , (4)

where J is the flux, D_o is free-solution diffusion coefficient, is porosity, and C/x is the concentration gradient (e.g., Lerman, 1979). Given a mean sediment porosity of 70% for the sulfate reduction zone (Paull, Matsumoto, Wallace, et al., 1996), sediment temperatures of ~4ºC (Ruppell, 1997), and a sulfate diffusion coefficient of 5.8 x 10^-6 cm s^-1 (5ºC, Li and Gregory, 1974), the sulfate gradients from Sites 994, 995, and PC 11-8 predict sulfate fluxes of (8.8, 8.2, and 18) x 10^-4 mmol cm^-2 yr^-1, respectively.

Mixing Model Results

An established approach of assessing the importance of AMO is to algebraically account for the carbon isotopic contributions of each component comprising the CO₂ pool (Blair and Aller, 1995). The CO₂ sources at the sulfate-methane interface include that from overlying seawater trapped within sediments during burial (sw), that derived from sedimentary organic matter during remineralization (om), and that produced by anaerobic methane oxidation (amo). In a closed system, the carbon isotopic composition of the pool at the SMI is related to its components by:

 ¹³C_{total pool} = (X_sw) (¹³C_sw) + (X_om) (¹³C_om) + (X_amo) (¹³C_amo), (5)

where X is the constituent's fraction of the total CO₂ pool, ¹³C is the carbon isotopic composition, and the subscripts sw, om, and amo refer to CO₂ donated from the sources listed above. For Site 995, the value of X_sw is fixed at 0.139 (seawater CO₂ concentration divided by CO₂ concentration at the SMI, or 2.3 mM/ 16.5 mM) with ¹³C_sw equal to 0. The isotopic value of sedimentary organic matter at the Blake Ridge averages -21 ± 3 PDB (N= 120; Brooks et al., 1983; Olsen, 1997), and this value is used for ¹³C_om. The isotopic composition of methane at the interface is -101 PDB (Hoehler et al., Chap. 8, this volume), and this value is used for ¹³C_amo (assuming no fractionation during AMO). The proportions of C_om and C_amo composing the remaining fraction of the CO₂ pool (1.0 - 0.139 = 0.861) are varied to produce the mixing line in Figure 4.

The mixing model estimates that ~24% of the carbon within the CO₂ pool at the sulfate-methane interface is derived from methane (Fig. 4). This is only a crude estimate because the system is open (i.e., CO₂ diffusion occurs), because carbonate mineral precipitation occurs (Rodriguez et al., Chap. 30, this volume), and because carbon fractionation occurs during AMO.

Diagenetic Model Results

Modeling of methane concentrations provides an independent estimate of the amount of sulfate consumed by AMO. Although in situ methane concentrations of deep-water sediments are difficult to measure accurately (Paull et al., unpubl. data), methane concentrations less than the methane bubble saturation at surface temperature and pressure should reflect in situ concentrations because loss of methane through outgassing is unlikely. Hence, the methane concentration data (Table 3) are apparently suitable for modeling.

The method assumes steady state conditions so that the distribution and magnitude of reaction rates can be solved for by fitting observed concentration data and solving the diagenetic equation (Eq. 3) for R_x using numerical methods. A cubic spline fit to the methane concentrations measured in Site 995 sediments (Hoehler et al., Chap. 8, this volume) approximates these data well (Fig. 5A). The measured methane profile has inflections (see arrows Fig. 5A), accurately reflected in the cubic spline fit, that produce variations in the first and second derivatives. The model results identify the depths where methane consumption and methane production are expected, and indicates the magnitude of the reaction rates as a function of depth (Fig. 5B). Model results also show that methane consumption occurs over a 2-m interval (~20.5-22.5 mbsf), and that methane production occurs immediately below (Fig. 5B). The modeled AMO reaction rates show peak values approaching 5 µM yr^-1 (0.005 µmol cm^-3 yr^-1) just below 21 mbsf.

The integrated methane flux corresponds to the area under the first derivative of the cubic spline fit (not shown). The model predicts a total upward methane flux of 2.9 x 10^-4 mmol cm^-2 yr^-1. At Site 995, the corresponding total sulfate flux, calculated using Fick's First Law, is 8.2 x 10^-4 mmol cm^-2 yr^-1. Thus, approximately 35% of the total sulfate flux into the sediment is used to consume upwardly diffusing methane.

Model results from fitting the methane concentration values agree well with concentration and isotopic data. As expected, the slight inflection in the concentration trend within the methanogenic zone (Fig. 5A) causes the model to predict a shift from methane production to methane consumption, and the large inflection in methane concentration at the SMI coincides with peak methane oxidation rates. Furthermore, minimum ¹³CCO₂ values are coincident with peak methane oxidation rates.