INTRODUCTION
The knowledge of the three-dimensional (3-D) structural and petrophysical properties of marine sediments is fundamental for many investigations towards the understanding of physical and chemical interactions of the ocean and the oceanic crust. The existence of a sediment cover overlying the ocean crust strongly affects fluid circulation between the ocean and the basement formation. Delineation of the thickness and structural stratigraphy of the sedimentary layer is important for determination of the hydrothermal flow patterns in the upper crust. The efficiency of this natural cover as a hydrothermal seal to the underlying active hydrothermal regime is largely defined by the sediment properties. The success of hydrothermal studies thus depends upon accurate knowledge of the in situ permeability, thermal conductivity, pressure, and temperature gradients in both the active hydrothermal regimes in the upper oceanic basement and the overlying sediment cover.
The physical properties of sediments and natural rocks are strongly influenced by environmental conditions, especially in situ pressure and temperature. Important among these physical properties are the porosity, bulk density, velocity, permeability, and thermal conductivity. Measurements of these properties made on the core samples in the laboratory need to be corrected for deviations from the natural in situ conditions. Another challenging problem is to estimate in situ properties in shallow high-porosity sediments that cannot be reliably measured in the laboratory. Accurate velocity-depth profiles under this condition allow for time-to-depth conversion of seismic reflection data. Velocity-depth profiles are used to assess the sediment/basement interfaces and other geological stratigraphic events (Davis et al., 1997) and to calculate porosity depth, thermal conductivity-depth profiles, and the subsurface thermal structure (Davis and Villinger, 1992). These relationships are usually approximated, however, by empirical or semiempirical models, and often by polynomial fits of field measurements (e.g., Hamilton, 1971; Jarrard et al.,1989; Davis and Villinger, 1992; Hyndman et al., 1993). In this report, we examine these relationships in a more general theoretical framework of poroelasticity. Such relationships may be applicable to different sedimentary environments of a wider porosity range.
We obtain high-resolution density-depth, porosity-depth, and velocity-depth profiles by combining the proposed theoretical model with a synthesis of three independent field measurements: core, log, and seismic data. The advantages of core-log-seismic integration is that these three independent measurements exploit different ranges of measurement frequency and investigate different scales of sediment property information. When integrated together, more reliable and complete knowledge of sediment properties is possible than when they are used separately.
Core measurements made under controlled conditions reveal the physical, chemical, and structural compositions and properties at the scale of the core sample. Shipboard measurements, such as those from the multisensor track (MST), provide high-resolution continuous records of these properties. Core measurements are especially useful at shallower depths where in situ logs cannot be recorded. At larger centimeter-to-meter scales, log data provide "ground truth" of in situ properties wherever the hole condition is reasonably good. Log data also bridge the resolution from the millimeter scale of core sample to the meter scale of seismic data. Although the seismic resolution is comparatively low, it is an efficient means to trace the events identified from the well-log data beyond a drilled site and to construct spatially continuous maps of physical properties. Constrained by log and core data, the seismic data provide an important tool for regional investigation. Integration of core measurements and downhole log data has been increasingly exploited for estimation of permeability and thermal conductivity in hydrological and hydrothermal studies. Villinger et al. (1994) estimate in situ thermal conductivity of sediments from downhole logs. Fisher et al. (1994) measure sediment consolidation parameters to define rebound corrections for shipboard measurements of physical properties, including in situ void ratio (or porosity) and bulk density. Fisher et al. (1994) also develop relationships between effective stress and void ratio and between permeability and void ratio by means of consolidation and permeability tests.
Moore et al. (1995) obtain good agreement of log-derived fluid pressures with estimates from consolidation tests for Ocean Drilling Program (ODP) Leg 156. Many attempts have also been made to estimate in situ properties of sediments and natural rocks by integration of log and seismic data for diagnosis of crustal evolution, the history of deformation processes, and paleoceanographic applications (Bloomer and Mayer, 1997). Recently, seismic data have been used to evaluate the petrophysical properties of the formation (Rasmussen and Maver, 1996). Seismic inversion of porosity also promises to provide "continuous" two-dimensional (2-D) and 3-D models of permeability and thermal conductivity. Core-log-seismic integration is, therefore, arguably the best means to analyze and interpret these three independent data sets. This integration effort may also help to achieve a better understanding of the underlying mechanism of interactions between wave and pore-scale structures of the sediments/rocks, if theoretical models are successfully developed to link the measurements to intrinsic properties of the sediments, rocks, and pore fluids.
To accomplish this, we use an extended Biot theory of poroelasticity as a unifying theoretical model, because it can potentially deal with cases where solid suspensions in fluid or isolated fluid inclusions in solid are important (Sun, 1994; Sun and Goldberg, 1997b). Furthermore, even a very simplified version, which reduces formally to the Biot or Gassmann model, offers considerable insights on how to define and analytically determine key model parameters. There are thirteen model parameters that need to be defined in the complete formulation (Stoll, 1989); in the reduced model, there are seven or eight model parameters (Gassmann, 1951a, 1951b; White, 1983; Hamilton, 1971; Jarrard et al., 1989). So many parameters cause immense difficulty for practical applications, and often misunderstanding (Stoll, 1998), because the frame bulk and shear moduli remain largely unconstrained for individual cases (Bryan and Stoll, 1988).
We propose two analytical formulas for these frame moduli. The proposed model has eight parameters, which can, fortunately, be defined through core-log-seismic integration. These model parameters are grain density, grain bulk and shear moduli, fluid density and bulk modulus, porosity, and bulk and shear coupling coefficients. The latter two coupling coefficients are defined as flexibility factors. The first five parameters are solid and fluid properties that can be estimated from core measurements. Porosity can either be obtained from well log or derived from the shipboard gamma-ray attenuation porosity evaluator (GRAPE) density records. The flexibility factors can be determined using sonic acoustic and shear logs. If these data are not available, they may be estimated using core and seismic data by generalized nonlinear inversion (GNI), which optimizes these parameters to minimize the discrepancy between field seismic data and the synthetic seismograms generated using the theoretical model.
The methodology adopted in this report is summarized as follows. The (A) steps are applied to the logged site, and (B) steps are applied to sites without logging. The equations used are defined and referred to in the following sections.
- Grain and fluid properties
Calculate the average grain and fluid properties from discrete index property (IP) and digital sonic velocimeter (DSV) measurements; namely, grain density and grain P-wave velocity (Vp) and S-wave velocity (Vs), and fluid density and velocity. Where the DSV measurements are poor, the grain velocities Vp and Vs may be calculated theoretically from the mineral compositions of the core sample (e.g., Jarrard et al., 1989) or from other resources.
- Bulk density
A. Edit the density logs for hole-condition corrections.
B. Edit the MST GRAPE density to ensure the data quality and eliminate unreasonable data points due to measurement errors. It is assumed that basic instrumental and environmental corrections have been routinely applied to the data (Boyce, 1976).
- Porosity
A. Edit the porosity logs for hole-condition corrections.
B. Generate pseudoporosity log using the corrected GRAPE density log, the average grain density and fluid density, and the density-porosity relation (Eq. 19).
- P-wave velocity
A. Edit sonic Vp logs for hole-condition corrections. Generate three crossplots: density and porosity logs, porosity and velocity logs, and density and velocity logs from separate runs, if available, to further reduce the effect of poor hole conditions. Also, generate an initial pseudovelocity log from corrected porosity logs using the proposed model with an initial value for the flexibility factor 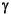 . Use the GNI scheme to optimize
. Use the GNI scheme to optimize 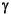 , minimizing the discrepancy between the true velocity log and the pseudovelocity log at the logged site.
, minimizing the discrepancy between the true velocity log and the pseudovelocity log at the logged site.
B. Use the final optimized flexibility factor 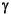 from the logged site as an initial
from the logged site as an initial 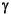 value, and use the data obtained in Steps 1-3 and Equations 17-23 and 27 to generate an initial pseudovelocity log.
value, and use the data obtained in Steps 1-3 and Equations 17-23 and 27 to generate an initial pseudovelocity log.
- Reflection-coefficient series
A. Calculate reflection series using the corrected density and velocity logs and Equation 29.
B. Calculate reflection series using the corrected density and pseudovelocity logs and Equation 29.
- Synthetic seismogram
Generate synthetic seismogram using Equation 30 and results from Step 5. The optimal center-frequency of the source wavelet can be estimated from spectral analysis of nearby seismic data.
- GNI scheme
A. Use the GNI scheme and Step 4A to make further corrections on Vp logs for possible mismatch in traveltime.
B. Use the GNI scheme to minimize the mismatch between the synthetic and field seismic data and optimize the flexibility factor 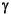 using Steps 4-7 iteratively. The optimal synthetic seismogram should have a better match with field data in traveltime and amplitude.
using Steps 4-7 iteratively. The optimal synthetic seismogram should have a better match with field data in traveltime and amplitude.
- Further GNI optimization
A. Use GNI scheme and repeat Steps 5-7 to optimize the source parameter and the center-frequency, and to obtain a better match of the synthetic with field seismic data in both waveform and amplitude.
B. Repeat Steps 4-7 to optimize the source parameter and the center-frequency, and to obtain a better match of the synthetic with field seismic data in both waveform and amplitude.
- Results
A and B. Obtain the optimal flexibility factor 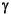 , source center-frequency, synthetic seismogram, and the optimal high-resolution pseudovelocity log.
, source center-frequency, synthetic seismogram, and the optimal high-resolution pseudovelocity log.
In the following sections, we present the theoretical model, the modeling results, and an analysis to illustrate the core-log-seismic integration method. Nine sites are studied along a transect extending more than 100 km eastward from the Juan de Fuca Ridge, drilled during ODP Leg 168 in 1996.
This transect penetrates sediments from a few meters to hundreds of meters thick overlying young oceanic crust of age 0.9-3.6 Ma in the eastern Pacific of 48°N (Fig. 1). To the best of our knowledge, it is the first time that good estimates of high-resolution porosity-depth and velocity-depth profiles have been used at sites without logging to construct synthetic seismograms in good agreement with field seismic data along such a long transect. We discuss the significance of the proposed velocity-porosity relationship and the important geological interpretation of the flexibility factor 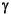 , which characterizes the softness or "uncompactedness" of the formation. We also point out some difficult problems that might be encountered in quantitative core-log-seismic integration aimed towards other sedimentary environments, such as the scale difference of core, log, and seismic data and the signal/noise ratio of seismic data.
, which characterizes the softness or "uncompactedness" of the formation. We also point out some difficult problems that might be encountered in quantitative core-log-seismic integration aimed towards other sedimentary environments, such as the scale difference of core, log, and seismic data and the signal/noise ratio of seismic data.

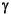 . Use the GNI scheme to optimize
. Use the GNI scheme to optimize 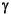 , minimizing the discrepancy between the true velocity log and the pseudovelocity log at the logged site.
, minimizing the discrepancy between the true velocity log and the pseudovelocity log at the logged site.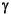 from the logged site as an initial
from the logged site as an initial 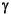 value, and use the data obtained in Steps 1-3 and Equations 17-23 and 27 to generate an initial pseudovelocity log.
value, and use the data obtained in Steps 1-3 and Equations 17-23 and 27 to generate an initial pseudovelocity log.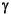 using Steps 4-7 iteratively. The optimal synthetic seismogram should have a better match with field data in traveltime and amplitude.
using Steps 4-7 iteratively. The optimal synthetic seismogram should have a better match with field data in traveltime and amplitude.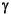 , source center-frequency, synthetic seismogram, and the optimal high-resolution pseudovelocity log.
, source center-frequency, synthetic seismogram, and the optimal high-resolution pseudovelocity log.