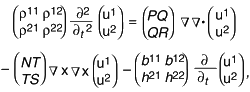(1)
Various investigations have developed empirical velocity-porosity relationships that are valid for only limited cases. The use of a time-average equation (Wyllie equation) to interpret sonic logs has been a standard practice in the oil industry for typical sedimentary rocks of intermediate (<40%) porosity (Wyllie et al., 1956; Schlumberger, 1989). Combining theoretical results from Gassmann theory of elastic waves in porous media with experimental ones from core, laboratory, and real seismic data, Hamilton gives many empirical relationships that have been used by many scientists in studies of marine sediments (Hamilton, 1971, 1976; Stoll, 1989; Jarrard et al., 1989; Hyndman et al., 1993; Sun et al., 1994; Guerin and Goldberg, 1996; etc.). Hamilton (1979) also reported Vp/Vs and Poisson's ratios in marine sediments. Sun (1994) developed a dynamical theory of fractured porous media that generalizes Biot theory and Gassmann theory of porous media. In this report, we briefly review this dynamical theory and outline a simplified version of it. This theory is expected to be valid for marine sediments over a wide porosity range and in different sedimentary environments.
The basic theory of seismic-wave propagation is founded upon the equations of motion of classical continuum mechanics. The structural effects of individual defects, pores, or fractures and related dynamic instability have been studied only as boundary-value problems. Natural materials, however, are mixtures of different minerals with complicated porous and/or fracture structures. It is the pores, cracks, fractures, fissures, joints, faults, and other internal structures that are the vital elements for the storage and migration of subsurface fluids. Many theoretical studies of seismic properties of porous or fractured media, such as effective medium theories (e.g., Kuster and Toksöz, 1974; O'Connell and Budiansky, 1974; Bruner, 1976; Hudson, 1980) and field theories (e.g., Kosten and Zwikker, 1941; Frenkel, 1944; Biot, 1956; Dvorkin and Nur, 1993), have been applied in experimental studies and in field examples with limited success. For example, the Biot theory (Biot, 1956), of which Gassmann theory is a special case, can be used phenomenologically to predict porosity from seismic velocities more accurately than the time-average equation (Wyllie et al., 1956), but physically cannot be used for rocks at low differential pressures (Gregory, 1976; Murphy, 1984; Sun, 1994). This limits the ability to obtain high-resolution petrophysical and stratigraphic information from seismic or well-log data. Biot theory of wave propagation in porous rock has gained increasing use in seismic reservoir modeling. However, the effects of fractures and cracks in natural rocks have been largely ignored in its development. To extend Biot theory, Sun (1994) developed a topological characterization of structural media that provides a representation of the internal structure of a fractured porous medium at a finer scale and investigated the general mechanics and thermodynamics of fractured porous media. This theory was intended to provide a unified theoretical model for the full porosity range of materials from low-porosity igneous rocks to highly unconsolidated sediments.
In very simple terms, a porous medium with or without fractures consists of solid matrix and pore fluid. The physical properties of the composite (the porous medium) is determined by knowing the intrinsic properties of the solid grains and pore fluid, the parameters characterizing the structural effects, and the coupling coefficients between the solid grains and between the solid matrix and fluid. For low-porosity rock, like granites, the velocity change with pressure is mainly caused by change of the internal structures (cracks) under pressure. With increasing pressure, pre-existing cracks become collapsed and new cracks begin to form. Theoretical calculation of seismic velocities against measurements can give quantitative evaluation of the dynamic changes of aspect ratio with pressure and delineation of the undergoing deformation process (Sun and Goldberg 1997b). For high-porosity sediments or sedimentary rocks, velocity change with pressure is caused mainly by change of mechanical coupling between solid grains and the coupling between the pore fluid and grains (Geertsma and Smit, 1961; Domenico, 1977; Sun et al., 1994; Sun and Goldberg, 1997a). With an increase in depth, and therefore in pressure, sandy sediments become more rigid as the interlocking between grains and coefficient of sliding friction are increased. High-porosity silty clays and hemipelagic mud also gain rigidity and tightness through cohesion. More accurate quantification and estimation of sediment/rock properties can be obtained by a more detailed characterization of these coupling effects.
The interactions occurring in a porous medium with or without fractures are mathematically described as coupled effective macroscopic wave fields consisting of individual, microscopic fields that interact globally through volume averaging. From both the dynamic and constitutive equations, an extended Biot theory for a two-phase fractured porous medium (neglecting the intrinsic viscoelastic effects of each individual phase) is derived:
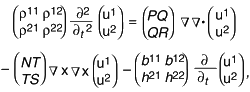(1)
where u1
and u2
are the solid and fluid displacements, respectively. The parameters in Equation
1 are dependent upon fundamental geometrical parameters 
ab
and 
ab
(a, b = 1, 2).
These geometrical parameters are functions of the topological invariants of
surfaces (or pore surfaces) and volume quantities. Physically, parameter ab
represents structural factors used to obtain an effective vector field such as
particle velocity from averaging the vector fields of individual phases.
Parameter ab
represents structural factors used to obtain an effective tensor field such as
stress from averaging the tensor fields of individual phases.
The detailed expressions of these quantities can be omitted for the practical applications in this report. P, Q, R, N, S, and T are also functions of intrinsic moduli of the solid and fluid.
For a two-phase isotropic
fractured porous medium, the geometric parameter ab
can be specified as
, (2)
where
is porosity (i.e., the volume fraction occupied by fluid), c1
is the content of solid particles suspended in fluid, and c2
is the content of fluid inclusions isolated in solid. However, the geometrical
parameter ab
is symmetric (i.e., 21
= 12,
and 12
is a real nonpositive number). And
ab
= 11a1b
+ 22a2b
(a, b =
1, 2), (3)
where 1
and 2
are defined as
, (a = 1,
2), (4)
and 
and 
are the intrinsic density of the solid and fluid, respectively. If it is assumed
that all the pores and fractures in a fractured porous medium are connected;
that, more strongly, the space occupied by each phase is connected (i.e., c1
= c2 = 0), then the tensor ab
is uniquely determined by porosity .
Using constraints on energy partition of relative motion and assuming that the flow in an individual pore is locally a Poiseuille flow, tensor bab (a, b = 1, 2) becomes
, (5)
where b is a constant,
, (6)
1
and 2
are the particle velocities of solid and fluid respectively, 1
= 11
+ 21,
2
= 12
+ 22,
and 
is the dynamic tortuosity defined as
, (7)
where 
is the angle between the velocity of the fluid and that of the solid. Therefore,
bab
(a, b = 1, 2)
are nonlinear functions of particle velocities of both solid and fluid phase.
The general wave equation, Equation 1, admits four kinds of elastic waves: the fast and slow P-waves and the fast and slow S-waves. This equation in its present form involves far more parameters than the Biot model, which represents the inherent properties of a fractured porous medium. As a forward problem, any given set of all these parameters specifies a concrete model. Nevertheless, it has to be simplified to be compared with experimental results and be practically useful. Because fluids do not possess intrinsic rigidity, it can be assumed that the intrinsic shear moduli of the fluids are negligibly small. By further assuming that the shear moduli acquired by fluids through coupling with the solids are also negligibly small, Equation 1 becomes
(8)
which is in the same form as the Biot equation of poroelasticity (Biot, 1956). The solution of this special wave equation admits three kinds of elastic body waves, namely, the fast and slow compressional waves and the shear wave. The notation used here in Equation 8 conforms to that used by Johnson and Plona (1982).
Although it is not
different from the Biot equation in its form, Equation 8 has an advantage that
all its phenomenological parameters can be defined explicitly in terms of the
fundamental geometrical parameters of the internal structures and the physical
parameters of the solid and fluid components. The shear modulus of the fractured
porous medium is expressed as a function of the shear modulus of the solid as
well as the geometry of internal structures. We assign 
ab
= cacb
and
, (9)
so that
, (10)
, (11)
, (12)
and
,
(13)
where
is the intrinsic shear modulus of the solid, and 
, 
, and p
are functions of the intrinsic bulk moduli of the solid (
) and fluid (
). P, Q, and R
are also explicit functions of the effective geometrical parameter ß.
The velocities of the fast P-wave (Vp+), slow P-wave (Vp-), and S-wave (Vs) from Equation 8 can be expressed explicitly using the above parameters as
, (14)
and
, (15)
where
, (16)
where 
and 
are the intrinsic mass densities of the solid and fluid respectively, fluid
content
= 
/
, and
is porosity. P, Q, and
R are also
explicit functions of the effective geometrical parameter
and ß. As expected, p,
ß, and tortuosity
depend upon aspect ratio and differential pressure, which characterize the
effects of the solid/solid and solid/fluid couplings on seismic waves.
Equations 14 and 15 have
been successfully used to investigate velocity-porosity and velocity-pressure
relationships for igneous and sedimentary rocks with porosities ranging from 1%
to more than 20% (Sun, 1994; Sun and Goldberg, 1997b). They can also be used to
estimate variations of aspect ratio with pressure from velocity-depth or
velocity-pressure profiles (Sun and Goldberg, 1997a). Even though the existence
of slow compressional wave in a water-saturated porous medium consisting of
fused glass beads has been proven in laboratory experiments (Plona, 1980), there
is not enough evidence that slow waves in natural marine sediments can be
observed (Stoll, 1998). Therefore, we consider only propagation of the fast
compressional and shear waves in sediments, and the two-phase medium can be
further simplified as an effective medium. To simplify our notations to those
commonly used in the literature, let s,
Ks,
and µs denote the density, bulk modulus, and shear modulus of the
solid grains respectively; and let f
and Kf
denote the density and bulk modulus of the pore fluid, respectively. Then
Equations 14 and 15 reduce to
(17)
and
, (18)
where
, (19)
, (20)
, (21)
, (22)
and
. (23)
The two parameters 
k
and µ
are bulk and shear coupling coefficients respectively. We call these coupling
coefficients the flexibility factors. They characterize the flexibility of the
skeletal frame when subject to compressional and shear motion, respectively. The
larger the values, the more flexible the frame for a given porosity, pressure,
and temperature. Physically, this implies that the harder the formation (better
coupling), the smaller the values of these flexibility factors. Note that the
parameters k
and Fk
can be interpreted as effective porosity and effective coupling factor for the
bulk modulus or for the compressional motion. Equations 20-22 can also be
derived from Biot or Gassmann equation by letting simply the frame bulk modulus
. (24)
Equations 23 and 24 can be
obtained using an analysis analogue to that given by Biot and Willis (1957),
assuming that the two parameters k
and µ
are not functions of porosity. In general, these two parameters are also
functions of porosity and other geometrical factors, and Equations 23 and 24
will be in more complicated forms. These two simple equations reveal
quantitatively how porosity and other geometrical factors affect the mechanical
responses of a porous medium to external motion. Equation 23 states that even
high-porosity unconsolidated sediments acquire rigidity that increases rapidly
as porosity decreases or pressure increases. This agrees with many published
works on the elastic properties of sediments (e.g., Hamilton, 1971; Stoll,
1989).
It should be noted that
Equations 17-23 define the compressional and shear wave velocities in terms of
intrinsic solid and fluid properties and geometrical factors, which are valid in
principle for the entire porosity range from pure solid (
= 0) to pure fluid (
= 1). However, when used in practice, caution should be taken because these
expressions have been obtained using many simplifications, even
oversimplifications. For example, the effects of solid suspensions in fluid and
isolated fluid inclusions in solid given in Equation 2 are neglected. This means
that both the connectivity of the fluid phase and the connectivity of the solid
phase are assumed to be perfect. In retrospect, however, Equations 23 and 24 can
be generalized to be suitable for many practical situations,
(25)
and
, (26)
where fk
and fµ
denote pure geometrical effects that are functions of pressure P,
temperature T,
porosity ,
and other geometrical factors G.
Whereas the more complicated formulation for bulk modulus in Equations 20-22 are
derived from the stress-strain relation of poroelasticity, the geometrical
effects on wave velocities are essentially characterized by Equations 23-26
for frame moduli in the context of Biot field theory. Equations 23-26
show that the resistance of a skeletal frame to shear motion has the same
expression as the resistance of the skeletal frame to compressional motion. This
may suggest that the dependence of shear modulus µ on geometrical factors and
that of frame bulk modulus Kb
could originate from the same causes due to the geometrical changes of internal
pore structures under pressure. Such dependence is physically and mechanically
different from that of gross bulk modulus K.
When measurements on shear wave velocity are not available, we assume, as a first-order approximation,
, (27)
or more generally,
. (28)
It means that the
Poisson's ratio of the skeletal frame under a jacketed test is the same as the
Poisson's ratio of the solid grain. Even though this agrees with common practice
in practical applications, this assumption needs to be scrutinized by
experiments and field data validation. We expect that it is applicable for
sediments and high-porosity rocks. However, independent measurements of shear
wave velocity are necessary to determine these flexibility factors for more
detailed analysis.We will use Equations 17-23 as the theoretical working model
for subsequent core-log-seismic integration. The intrinsic solid and fluid
parameters (total of five) will be taken from core measurements. Porosity will
be obtained either from well log or derived from shipboard high-resolution GRAPE
density records with corrections for in situ conditions. Because there is no
shear wave log and only core measurements available at the drilled sites of ODP
Leg 168, the constraints on the shear flexibility factor µ
are inadequate. We will use the approximation formula in Equations 27 or
28 in the absence of these constraints.
