MODELING RESULTS AND DATA ANALYSIS

The sedimentary section drilled at nine sites during ODP Leg 168 provides an ideal opportunity to investigate the elastic properties of marine sediments. These nine sites span a 100-km transect on the east flank of the Juan de Fuca Ridge (48°N; Fig. 1). The depth of the sedimentary section varies from a few tens of meters to more than 500 m. The sediments encountered at all sites are composed mostly of interbedded sequences of hemipelagic mud (clayey silt to silty clay), sand turbidites, and silt turbidites (Davis et al., 1997). The deepest hole drilled during this leg is at Site 1027 where hemipelagic mudstone ~100 m thick was recovered below sandy and silty turbidites, before reaching basalt talus within thin interbeds of pelagic and hemipelagic mudstone at a depth of 569 m below seafloor (mbsf). The underlying basaltic basement ranges from 0.9 to 3.6 Ma eastward along the transect (Fig. 1).

Hole 1032A was the only hole logged during ODP Leg 168. It is located at 47°47´N, 128°07´W and was drilled to 338.4 mbsf and reached basement at 290.29 mbsf. Coring began at 184.53 mbsf, and the hole was logged to 283.9 mbsf. Bridging problems in the deeper part of the section thwarted all efforts to log deeper. Both the caliper log and heave record indicate a fairly good drilling environment and hole conditions through out the logged section (28- to 30-cm hole diameter), except in the deeper part of the hole. The density log (Fig. 2) was recorded using Schlumberger high-resolution hostile environment lithodensity sonde (HLDS) with 2.5-cm sampling interval.

The neutron porosity log was recorded using Schlumberger high-resolution accelerator porosity sonde (APS) with 5-cm sampling interval. The sonic velocity log (V_p) was recorded by the long-spacing array of the Schlumberger digital sonic tool (SDT) with sampling resolution of 15 cm. The overall quality of the log data is quite suitable for core-log-seismic integration, except in a few depth intervals where hole conditions were poor. Using the density and V_p logs, the seismic reflection coefficient (RC) series can be calculated as

, (29)

where Z_i = _iv_i is the acoustic impedance, and _i and v_i are the density and velocity at the discrete depth i, respectively. This r_i series in depth can be converted to a series r_n in two-way traveltime using the velocity profile. The latter is then convolved with a waveform to obtain a synthetic seismogram,

, (30)

where w is the wavelet and y is the synthetic seismogram. We use Ricker wavelet characterized by a single parameter, center-frequency, for the source waveform to generate synthetic seismograms in this report.

In Figure 2, the synthetic seismogram is compared with the shotpoint data from near Hole 1032A. The shotpoint seismic data were collected in 1995 by the University of Bremen, Germany. A 1.5-L (90 in³) generator-injector (GI) gun source was used for the seismic source. The gun was supplied with compressed air at a pressure of 11.72 MPa and fired at 25-m shot spacing at nominally 10-s intervals. The data were acquired digitally with 20-bit floating point resolution at 6-kHz sampling frequency and then low-pass filtered and recorded at 2-ms sampling interval (Davis et al., 1997). Because these single-channel seismic data have a high signal/noise ratio, as seen on the 2-D section, no noise reduction filtering was applied, and the original amplitude information is preserved as much as possible. The synthetic seismogram is generated iteratively using a generalized nonlinear inversion algorithm (GNI; Press et al., 1992). The center-frequency of the Ricker wavelet is optimized to obtain a best fit between synthetic seismogram and the field data by assuming initially that the impedance model derived from the logs is fairly accurate. The initial center-frequency of the wavelet is estimated using spectral analysis of the field seismic data to be about 40 Hz. The seismic traveltime and amplitude of the synthetic are controlled by impedance contrast between subsurface layers. Because no cores or logs are available above 74.83 mbsf, no synthetic seismograms can be generated above this depth with the exception of the seawater/seafloor reflection. This is simulated by specifying = 1.7 g/cm³ and v = 1665 m/s for the sediment at depth 0 mbsf. Note that the seismograms have been converted to depth in all the following illustrations, unless specified otherwise.

The comparison of synthetic data with the field trace in Figure 2 is generally of high quality. In two intervals indicated on the figure, poor hole conditions precluded a good correlation. For the interval below 200 mbsf, we use both moving-window averaging and density-V_p crossplot to make corrections on the sonic and density logs. Both the corrected density and velocity logs are shown in Figure 3. The corrected density and V_p logs are converted to reflection coefficients using Equation 29, and a synthetic trace is then generated using Equation 30. The RC series is fed into the GNI scheme to check the mismatch between the field seismic trace and the synthetic. The corrected synthetic seismogram agrees with field seismic data much better in the deeper part of the hole than in Figure 2. To estimate the porosity in these intervals, the corrected density log and the known average grain and fluid densities, _s = 2.68 g/cm³ and _f = 1.04 g/cm³, are used to generate a corrected porosity log below 200 mbsf. In Figure 3, both the corrected density and porosity profiles agree very well with discrete laboratory IP measurements. The laboratory DSV measurements of P-wave velocity, however, are lower than downhole sonic V_p log.

To ensure that the corrected density, porosity, and velocity logs are consistent, we extend this derivation of porosity from the density over the entire logged interval from 80 to 272 mbsf. A pseudoporosity log is shown in Figure 4 and generally agrees well with the downhole porosity log (except in the intervals of borehole washout). We use the pseudoporosity log and the theoretical model to calculate a predicted P-wave velocity. This is achieved by using the GNI scheme to optimize the error between the V_p log and the predicted P-wave velocity for an optimal flexibility factor 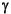. The estimate flexibility factor 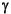is 7.0 at this site. For a more accurate analysis, 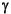should vary with depth. As shown in Table 1, the 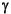value at this site is the lowest among the nine sites, which indicates that the sediment column at this site is the most compacted of those drilled during Leg 168. The model parameters needed for the theoretical calculation of the V_p and synthetic seismogram are also summarized in Table 1. The predicted V_p from this calculation approximates the downhole V_p log well and is shown in Figure 4. It also agrees well with the seismically corrected V_p log for the depth interval below 200 mbsf (see Fig. 3). Figure 4 also shows that the synthetic seismogram generated using the pseudovelocity log matches the field seismic trace. Figure 5 indicates that the shipboard-measured GRAPE density agrees well with the downhole density log below 180 mbsf. This suggests that GRAPE density measurements need fewer corrections than velocity measurements performed in the laboratory.

Core-log-seismic integration at Hole 1032A illustrates that (1) seismic measurements can be used to aid log correction, (2) the theoretical model of depth- (or pressure-) dependent velocity-porosity relationships is valid for the sedimentary environment at this site, and (3) the same methodology may be usefully applied where there is no downhole velocity log.

Figure 4 and Figure 5 suggest that GRAPE density data could be used to derive high-resolution porosity-depth and velocity-depth profiles at the other eight sites where there are no logs. Caution must be advised in applying this model at all the sites and to all the seismic data in this area because local in situ parameters are required as input into this model. The seismic source waveform should also be optimized site by site. In the following, we use two holes, Holes 1023A and 1027B, to illustrate the generalization of the method. These two holes are at the opposite ends of the transect (Fig. 1) and are separated from each other by about 80 km.

Figure 6 shows GRAPE density records and pseudoporosity and pseudovelocity profiles compared with discrete IP and DSV measurements at Site 1023. Excellent agreement is obtained between synthetic seismogram and field seismic trace in both traveltime and waveform amplitude in the entire sediment column. The high-resolution density, pseudoporosity, and pseudovelocity profiles obtained also agree well with the IP and DSV measurements below the depth of 130 mbsf. Figure 6 indicates that the elastic rebound corrections made on these IP and DSV measurements were underestimated above this depth and require correction before use for other purposes.

Results from Site 1027 are shown in Figure 7. GRAPE density records and pseudoporosity and pseudovelocity profiles are compared with discrete IP and DSV measurements. Reasonable agreement is also achieved between the synthetic seismogram and field seismic trace except at the depth interval from 100 to 240 mbsf where almost no core was recovered. The agreement between the synthetic and field seismic data for Hole 1023A (Fig. 6) and for Hole 1032A (Fig. 4) is much better than that at Site 1027. Although the traveltime and seismic amplitude agree well, the waveform does not match. The lack of core data in intervals where such discrepancies occur causes this disagreement. Instead of interpolating physical properties over these intervals, we infer the properties of sandy sediments to predict the traveltime and amplitude in the synthetic. Reasonable agreement with the field seismic data is possible; however, the high-resolution impedance changes are still lacking in these intervals. Where cores were recovered below 150 mbsf, density, pseudoporosity, and pseudovelocity profiles match with the core IP and DSV measurements. DSV measurements below 450 mbsf are generally higher than the pseudovelocity data. It is interesting to note that the velocity-porosity relationship in the model used is better than either Wood's model or Wyllie's model in representing these data (Fig. 8).

With successful integration of core-log-seismic data at these three holes, we gain confidence to apply our methods to the rest of the sites of ODP Leg 168. Figure 9 shows the GRAPE density records for the nine drilled sites. Site 1031 is omitted because it is very near to Site 1030. The pseudoporosity profiles and pseudovelocity profiles for all these sites are shown in Figure 10 and Figure 11, respectively. Both these density-derived profiles have a sample interval of 5 cm. Figure 12 shows comparisons between synthetic seismograms and field seismic profiles at all sites, plotted in two-way traveltime. Overall, these profiles all agree reasonably well. Table 1 summarizes all the model parameters that are needed to obtain the porosity-depth and velocity-depth profiles at all sites. The average grain density measured on core samples from a given site is used for that site, without accounting for the mineral compositions, which needs to be improved for a more detailed analysis. Note that the grain densities averaged from core measurements for Holes 1030B, 1028A, 1029A, 1027B, and 1032A range from 2.70 to 2.75 g/cm³, which are much higher than the average values expected for these sediments. A density of 2.68 g/cm³ is used for these sites instead. The fluid densities are 1.040 g/cm³, which is a good approximation for seawater at these depths (Pond and Pickard, 1978). The compressional and shear wave velocities of the solid grains are also assumed to be constant for all sites, which may not be necessarily accurate to estimate the grain elastic moduli. The estimated flexibility factor 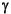for each site is also given. As the sediment thickness increases eastward from Site 1023 to 1027, the estimated flexibility factor 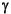in this model decreases (see Table 1), which implies that the overall sediment column becomes tighter or more compacted from Site 1023 to 1027. The implications of these results are discussed below.