-
. (1)
The tendency of calcium carbonate to precipitate can be inferred from simple mass balance calculations applied to the composition of sediment pore waters. For example, it has been shown for Hydrothermal Transition Sites 1023, 1024, and 1025 (Davis, Fisher, Firth, et al., 1997) that the increase in alkalinity in sediment pore waters is lower than the decrease in sulfate concentration expected from the stoichiometry of the reaction of organic matter oxidation:
. (1)
This low alkalinity increase is attributed to calcium carbonate precipitation. Thermodynamic calculations allow temperature, pressure, and solution composition to be combined into a single parameter (mineral saturation indices or free energies of reaction) to determine the mineral-solution reactions likely to control the composition of interstitial fluids.
The thermodynamics of the carbonate system in the ocean has been given very wide attention because of the primary importance of the carbon budget on global geochemical cycles. A computer program called CO2SYS was developed to calculate inorganic carbon speciation in seawater (Lewis and Wallace, 1999). The code allows the user to choose between different pH scales. It incorporates various models and formulations of the thermodynamic constants for the carbonate system. An important feature of the CO2SYS development is that the authors have crosschecked the relevant primary literature and corrected errors found in articles.
Almost all aqueous carbon dioxide models included in CO2SYS rely on a description of the CO2 system based on apparent stability constants measured in standard seawater as a function of temperature, pressure, and salinity at oceanic conditions (i.e., at temperatures from -1° to ~40°C, pressures to 1000 bars, and salinities to 40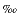
). In situ pressures in the Leg 168 sediments are hydrostatic and around 300 bars, but temperatures can reach 63°C. Calculations using CO2SYS above 40°C require that the expressions for the apparent constants for the carbonate system and for calcium carbonates be extrapolated beyond their intended range of application. Also, although measured salinities are close to 35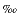, sediment pore waters collected during Leg 168 are not standard seawater; they are depleted in Mg and enriched in Ca (Davis, Fisher, Firth, et al., 1997). We assume that composition changes implied by the replacement of Mg by Ca do not induce large changes in the thermodynamic properties of the aqueous solution.
The saturation state of the pore waters with respect to calcium carbonates can be inferred from the values of the calcite and aragonite saturation indices at in situ temperature and pressure. The calcium carbonate apparent ionic product (Q*) is the product of the measured calcium concentration by the carbonate concentration calculated from measured pH and alkalinity values
, (2)
in which m is the molality of the designated species. The saturation index (SI) is defined as the ratio of the calcium carbonate apparent ionic product to the apparent solubility product of the considered solid (calcite or aragonite)
. (3)
The SI is related to the free energy (or chemical affinity, A) of the dissolution reaction of the considered mineral by
, (4)
where R is the gas constant and T the absolute temperature. The solution is undersaturated when A is negative (minerals can dissolve) and supersaturated for positive values (minerals can precipitate). Using the free energy of reaction instead of the saturation index expands the undersaturated side of the plotted data and reduces the supersaturation side (Fig. 2, Fig. 3).
Values of the affinity of the dissolution reaction are always greater for calcite than for aragonite (Fig. 3). This reflects the greater stability of calcite when compared to that of aragonite: the driving force for dissolution is greater for aragonite, and the driving force for precipitation is larger for calcite. This is one cause of the well-known recrystallization of calcium carbonate: dissolution of aragonite and precipitation of calcite. The difference between the affinities of reaction for calcite and aragonite are small (about 0.4 kJ/mol) compared to the scatter of the data depicted in Figure 3. It is impossible to distinguish between calcite and aragonite at this level of accuracy.
Because pH on board the ship was measured on the NBS pH scale, we retained this option throughout all this work. Data plotted in Figure 3 shows that pore-water pH values are scattered over a range that can reach up to 0.5 pH units. A few samples of the sediment from Leg 168 were squeezed to extract the pore waters 4 hr after core recovery (the so-called "post-MST" samples in table 16 of Davis, Fisher, Firth, et al., 1997), whereas the usual procedure was to process the samples in the chemistry lab immediately after recovery (i.e., within an hour). The difference in pH and alkalinity of these samples with those squeezed right after recovery is small but noticeable. This pH difference is comparable to the pH scatter of the whole data set, but alkalinity is lower, indicating active calcium carbonate precipitation within the samples following recovery. This sampling artifact contributes to the scatter in the pH data (Fig. 3). We calculated the distribution of carbonate species for the laboratory pressure and temperature at which the pH and alkalinity determinations were made, as well as for in situ conditions to verify that late analysis does not lead to major changes in the affinity of reaction. We checked that neither calcite nor aragonite are at equilibrium with the pore waters at the shipboard conditions (20°C and 1 bar). Results indicate that pore waters are largely supersaturated at these conditions.
We used the composition of the Baby Bare spring water (Mottl et al., 1998) to calculate the variation of the affinity of the calcite dissolution reaction implied by the use of different aqueous carbon dioxide models (Lewis and Wallace, 1999). Figure 2 shows that the results obtained with these various models are quite consistent (within 0.1 kJ/mol of each other) up to a temperature of about 30°C. Beyond this temperature, the "Geosecs" model leads to an unrealistic trend in the affinity of reaction. Other models are consistent within 0.2 kJ/mol up to about 60°C and show smooth variations of the affinity of reaction with temperature, as can be expected. We retained the "Dickson and Millero" option throughout this work. In these calculations we assume that pH does not change with temperature. Figure 2 also shows that the supersaturation of the Baby Bare spring waters with respect to calcite decreases when temperature decreases. These waters are venting to the deep ocean at 25°C, having cooled from an estimated temperature of 64°C during their ascent (Sansone et al., 1998). Our calculations are consistent with the removal of carbon from the spring waters by active calcium carbonate precipitation in the igneous basement at temperatures higher than that of the venting fluids, as concluded by Sansone et al. (1998).
