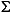RESULTS

To provide a simplified overview of the fine-fraction grain-size frequency distribution of the data set, we have chosen a three-dimensional contour presentation that incorporates all samples with their individual frequency distributions (Fig. F6). The original data set was gridded to a 1-m depth and 20-k.y. age grid resolution, with linear interpolated size classes of the original 31 channels in micrometers. We applied a true two-dimensional zero-phase filter algorithm to smooth the data (the moving average filter has a size of five data points for the age or depth axis and three points for the grain-size axis). The contour algorithm is linear and resolves six levels representing the percent of sediment found for each grain-size class. Percent values refer to the total sediment sample dry mass. The >63-µm size fraction was added as an undifferentiated two-dimensional summary curve at the right side of the graph. Single data values and a zero-phase filtered curve, obtained with a one-dimensional filter (five point) of the same size as for the fine fraction, are given. The fine-fraction and smoothed coarse-fraction data are therefore in phase and have identical interpolated depth resolutions.

In general, the grain-size distribution downcore shows significant variations (Fig. F6). There are five prominent intervals in which cyclicity and the clay/silt ratio change drastically: (1) between 0 and 40 mcd (0 and 1.3 Ma), (2) between 40 and 80 mcd (1.3 and 2.4 Ma), (3) between 80 and 220 mcd (2.4 and 6 Ma), (4) between 220 and 360 mcd, and (5) below 360 mcd (prior to 8.1 Ma).

Interval 1 is characterized by small-scale variations and a pronounced dominance of the 5-µm size class fraction compared to the other identified intervals. Even though the overall grain-size distribution within this interval is very fine, interval 1 is also associated with a continuous tail of 1% of the distribution reaching the 40-µm fraction.

Interval 2 shows a steady increase in the dominant grain-size class and only small-amplitude cyclic variations. Interval 2 terminates with the highest dominant grain-size classes with 20 to 40 µm and 5% loading of our data set. The steady increase toward these highest recorded values seems to be interrupted between 60 and 70 mcd (~2.3 Ma). We attribute this gap in the temporal and spatial continuity of the grain-size distribution to the hiatus (discussed in Hillenbrand and Ehrmann, Chap. 8, this volume).

Interval 3 is characterized by very high amplitude and frequency cyclic distribution changes and a more or less steady decline in the grain-size mode and overall amplitude. High loadings of up to 4% for the 20-µm window are reached in the middle of this interval at 135 mcd (4.3 Ma).

Interval 4, ~220 mcd (6 Ma), starts with a very narrow spectral distribution combined with high loadings of 6% in the size class below 5 µm. This nearly symmetrical upper zone of interval 4 has no tails into the coarser class fractions. The remaining lower part of the interval is characterized by a steady increase toward coarser size classes and moderately frequent but high-amplitude variability, especially in the coarser tail (>25 µm) of the grain-size spectra.

Interval 5, starting at ~360 mcd (8.1 Ma), shows the same cyclic pattern as interval 4, but with a decreasing trend in the occupied size classes.

The plot (Fig. F6) allows us also to check if the fine fraction (<63 µm) is locally affected by ice-rafted debris (IRD) events. These are suspected where the <63-µm fraction tails seem to be connected to peaks of the >63-µm fraction. (see Cowen, Chap. 10, and Wolf-Welling et al., Chap. 15, both this volume, for further IRD and coarse-fraction data).

Mean (1st moment)

= f · m/N,

Standard Deviation (2nd moment)

= SQR[f (m -)²/100],

Skewness (3rd moment)

Sk = f (m -)³/100³, and

Kurtosis (4th moment)

K = f (m -) ⁴/100⁴,

where

f = weight percent (frequency) in each grain-size grade present,

m = midpoint of each grain-size grade (in values), and

N = total number in sample; 100 when f is in percent.

For further general investigations, we applied the method of moments for the <63-µm data set. The weight percent of the fine fraction was hereby recalculated to 100%. The method of moments is well established (Griffith, 1967; Folk, 1974; Boggs, 1987) and is the mathematical expression of four characteristics of a quasi-Gaussian distribution. In this case, the moments are calculated using values. The skewness (third moment) and kurtosis (fourth moment) express the deviation of a grain-size frequency distribution from the general assumption of log normality to the base of two (Friedman, 1962). The results for the <63-µm range are given in a filtered (zero-phase low-pass filter) (Fig. F7) and discrete versions (Fig. F8). The filter has been applied after interpolating the data to constant depth and age resolution. The aim of this filtering procedure was to reduce the effects of uneven sampling spacing. A documentation of the frequency response and the resolution in time and distance of the Chebyshev filter algorithm (Rabiner and Gold, 1975) used is given in Figure F7.

Particle-size data are presented as downhole plots vs. depth and age of bulk <63-µm fraction in weight percent of the total dry sample mass, mean (first moment), standard deviation (second moment), skewness (third moment), and kurtosis (fourth moment). Bulk fine-fraction contents are generally high (>95 wt%). The mean of the bulk fine fraction (<63 µm) varies between 7 and 9.2 units. There are some prominent maxima around 80 mcd (2.8 Ma), 138 mcd (4.4 Ma), 250 mcd (6.2 Ma), 290 mcd (6.8 Ma), 340 mcd (7.8 Ma), and 420 mcd (8.8 Ma). It appears that the mean of the fine fraction (<63 µm) is generally decoupled from the coarse fraction. Only in two cases, at 340 mcd (7.8 Ma) and 70 mcd (2.27 Ma), does a high mean of the coarse fraction correlate with a higher content of coarse fraction (>63 µm). Average standard deviation values above 1 indicate poor sorting of the <63-µm fraction (Folk, 1974). The standard deviation and mean of the fine fraction in units are inversely correlated throughout our data set. A decrease in degree of sorting is apparently coupled with higher mean grain-size values. The skewness values vary between -0.2 and >2. The skewness is, with a few exceptions, positive. This means that almost all samples analyzed have excess fine particles with respect to a log normal Gaussian distribution. There is a positive correlation between the skewness values and the kurtosis values. Fluctuations within the kurtosis values (measure of the peakness of a distribution) indicate highly variable depositional processes (Friedman, 1967).

The initially defined intervals, based on the overall appearance of the grain-size distributions in contour representation, also show distinguishing features in their moment representation. A detailed description is beyond the scope of this report, but some marked changes are noteworthy (e.g., the change in skewness and kurtosis between interval 2 and 3 or the time around 6 Ma [end of interval 3 and beginning of interval 4], where mean grain sizes reach a minimum that is combined with moderate sorting and low skewness and kurtosis values).

Not all of the <63-µm fraction is equally meaningful for the evaluation of depositional energy or paleocurrents. The special importance of grain-size parameters such as the sortable silt fraction (10-63 µm) as a percentage of the fine fraction (McCave, 1995a, 1995b), and the mean of the 10-63-µm fraction (McCave, 1995a) are especially current sensitive. Therefore, we applied the same statistical treatment (method of moments) to the sortable silt fraction (10-63 µm). Sortable silt fraction mean (first moment), standard deviation (second moment), skewness (third moment), and kurtosis (fourth moment) are presented as downhole plots vs. depth and age (Fig. F9). The data presented are unfiltered and uninterpolated to give a better idea of data density and data gaps. Sortable silt fraction values are generally much lower (average ~30 wt% of the fine fraction) than the bulk fine-fraction values, emphasizing the large fraction of <10-µm sediment not accounted for (Fig. F9; left column). In addition, the amplitude of fluctuation in the sortable silt fraction (10-63 µm) appears to be much higher in older sediments (below 280 mcd [late Miocene]). However, this may be the effect of higher sample density in this interval. The mean of the sortable silt fraction indicates that most of the sortable silt fraction has a grain size of ~6 units (15 µm), whereas the minimal mean values range below 5.4 units (25 µm).

As a result of removing the fine-grained tail below 10 µm, most of the skewness values turned negative in the sortable silt statistic. After this modification, frequency distributions that originally had a nearly symmetrical distribution appear to be coarsely skewed.

Assuming that grain-size characteristics in the sortable silt range reflect conditions of the depositional process or environment, we used the statistical parameters determined by the methods of moments (Fig. F7) to group our data set. In contrast to previous approaches (Friedmann, 1961, 1967, 1979) that apply environmental statistical analyses to distinguish depositional settings (e.g., beach from river sand), we used bivariant plots to define depositional processes within a single depositional environment.

The best spatial separation of our sediment drift data set is in the bivariant plots: mean vs. skewness (Fig. F10A) and standard deviation vs. skewness (Fig. F10B). Three clearly separated populations are seen. Population 1 is characterized by the highest absolute mean grain sizes and standard deviation (Fig. F10C). Population 2 shows high variability in skewness and only small variations in mean grain size and standard deviation (Fig. F10A, F10B). Population 3 is characterized by the lowest mean and standard deviation values but displays the highest combined variability for the parameters skewness and standard deviation within the bivariant field (Fig. F10B, F10C). In general, samples with larger mean grain sizes have a higher standard deviation in our data set (Fig. F10C).

For a further visual inspection of the described populations we calculated average grain-size distributions for each population of the sortable silt (Fig. F11A) and for the <63-µm fraction (Fig. F11B). On average, populations 2 and 3 follow a unimodal distribution. In contrast, the average distribution of population 1 is very broad and bimodal. The average distribution plot for the sortable silt fraction (Fig. F11A) illustrates the characteristics of the three populations in a more graphical way.