METHODS
Standard triaxial tests are symmetrical compression tests on cylindrical samples, primarily performed to determine the shear strength of a material. The experiments were carried out using an ELE Tritest 50 setup, with a maximum cell pressure of 1700 kPa and maximum vertical load of 7500 N (Fig. F1). The horizontal stresses ( 2 =
2 =  3) are imposed by water pressure; the vertical stress (
3) are imposed by water pressure; the vertical stress ( 1) is imposed by piston load and water pressure (
1) is imposed by piston load and water pressure ( 1 = F/A +
1 = F/A +  3, with F = piston load and A = area). The water used for external and internal application of pressure to the specimen has to be de-aired to avoid measurement errors due to compressibility of the gaseous phase. The cylindrical triaxial cell encloses the specimen, which is installed on the cell base. The cell base contains the influx to and drainage off the cell and the specimen (Fig. F1). The outlets and inlets are each equipped with electrical sensors and connected through piping with either hydraulic pumps (water supply) or with measuring devices (volume change unit and pressure gauges).
3, with F = piston load and A = area). The water used for external and internal application of pressure to the specimen has to be de-aired to avoid measurement errors due to compressibility of the gaseous phase. The cylindrical triaxial cell encloses the specimen, which is installed on the cell base. The cell base contains the influx to and drainage off the cell and the specimen (Fig. F1). The outlets and inlets are each equipped with electrical sensors and connected through piping with either hydraulic pumps (water supply) or with measuring devices (volume change unit and pressure gauges).
The tests were carried out according to the instructions and recommendations for the determination of shear strength given by the German Institute for Standardization (DIN 18 137, 1990; see parts 1 and 2) and are characterized by three stages: (1) saturation, (2) consolidation, and (3) compression. Saturation pore pressure is a kind of passive pore pressure induced in the specimen by a hydraulic pump. The pore pressure during consolidation and compression stages is defined as back pressure, as it rises in the tested specimen as a reaction to cell pressure and piston load.
Basically, a series of three tests at different confining pressures must be conducted to construct the Mohr-Coulomb envelope in the shear stress (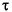 ) vs. normal stress (
) vs. normal stress ( n) diagram. Limited sample volume, due to fracturing and required sample size, restricted the number of tests per whole-round sample to only two at different cell pressures, or even only one. This circumstance reduces the accuracy of Mohr-Coulomb envelopes and makes determinations of shear parameters less precise.
n) diagram. Limited sample volume, due to fracturing and required sample size, restricted the number of tests per whole-round sample to only two at different cell pressures, or even only one. This circumstance reduces the accuracy of Mohr-Coulomb envelopes and makes determinations of shear parameters less precise.
As mentioned before, failure of the sample is induced by a piston advancing at constant speed (for velocities for each sample see Table T1), causing increasing vertical stress ( 1). The development of the vertical force is measured by a load transducer. The tests are run until an ultimate condition is reached (Head, 1986). Failure criteria can serve both the peak differential stress, where shear strength of the sample is exceeded, or a limiting strain of 15%-20% for plastically deforming soils. The axial shortening is measured by a strain-gauge sensor (Fig. F1). During undrained tests, the drainage system is locked and a pore pressure builds up as a result of compression. The vertical load and the displacement of the piston are measured by the load transducer and strain gauge sensor in time intervals, depending on the amount of change of these quantities. Except for the deepest sample from Site 1151, the strength of which exceeded the limit force of the load transducer unit, all tests were carried out until the failure criteria were reached. Two samples from Section 186-1151A-84R-2 were analyzed using drained shear tests because of temporarily defective testing conditions. On the one hand, the stiffness moduli obtained are comparable to those of the undrained tests, but on the other hand, we could not infer the cohesion and the internal angle of friction.
1). The development of the vertical force is measured by a load transducer. The tests are run until an ultimate condition is reached (Head, 1986). Failure criteria can serve both the peak differential stress, where shear strength of the sample is exceeded, or a limiting strain of 15%-20% for plastically deforming soils. The axial shortening is measured by a strain-gauge sensor (Fig. F1). During undrained tests, the drainage system is locked and a pore pressure builds up as a result of compression. The vertical load and the displacement of the piston are measured by the load transducer and strain gauge sensor in time intervals, depending on the amount of change of these quantities. Except for the deepest sample from Site 1151, the strength of which exceeded the limit force of the load transducer unit, all tests were carried out until the failure criteria were reached. Two samples from Section 186-1151A-84R-2 were analyzed using drained shear tests because of temporarily defective testing conditions. On the one hand, the stiffness moduli obtained are comparable to those of the undrained tests, but on the other hand, we could not infer the cohesion and the internal angle of friction.
According to the size of the cell's base, the samples had diameters of 35 mm. However, as most of the cores from Site 1150 underwent postdrilling stress relaxation (Figs. F2, F3), in most cases, only cylinders with diameters of 24 mm could be carved out. Sample preparation included sawing of the whole-round cores into pieces of required length, which amounted to 2-2.5 times the diameter. With the aid of a hand-operated soil lathe, the samples were cut and rasped into a cylindrical shape with a constant diameter of 35 mm (Head, 1982). Specimens with diameters <35 mm had to be prepared without the lathe. The top and bottom surfaces of the cylinders had to be cut off evenly and parallel to each other to avoid strain concentrations at the piston/specimen interface (Jaeger and Cook, 1979). The sample preparation had to be done very carefully to avoid disturbance of texture and cohesion. Before being installed into the cell, the specimen was wrapped in filter-paper side drains. Afterward, porous disks were fitted to both ends of the filter-wrapped cylinder before it was inserted into an impermeable rubber membrane. This drainage assemblage allowed an optimum of water flux in a vertical as well as horizontal direction and a homogeneous distribution of pore water pressure. With the setup and sample preparation described, a natural-rock surrounding could be roughly modeled. Parallel to the preparation of the cylinders, the water content and grain density were determined (Table T1). Porosity data were simply adopted from the shipboard measurements (Sacks, Suyehiro, Acton, et al., 2000).
After the sample was installed in the cell and connected to the top and base drainage system (Fig. F1), the cell and the connecting pipes were flooded with de-aired water. The general procedure of a CU test is as follows:
- A defined and reproducible stress state is established in the specimen by saturation and consolidation.
- The drainage system is closed.
- Vertical load is increased by continuously displacing the piston downward.
The aim of saturation is to dissolve remaining air in the pore water. Air in the pores corrupts the results of the compression test. To achieve saturation, the cell pressure and the pore pressure are increased simultaneously. The value of necessary saturation pore pressure depends on the initial saturation (S0) of the material tested:
-
S0 = (w
 s [1 - n])/(n
s [1 - n])/(n w)
w)
where
-
S0 = initial saturation;
-
w = water content (percent);
-
 s = grain density (g/cm3);
s = grain density (g/cm3);
-
n = porosity (percent); and
-
 w = density of water (g/cm3).
w = density of water (g/cm3).
According to DIN 18 137 (1990) part 2, initial saturation S0 between 0.65 and 0.9 requires a saturation pore pressure between 200 and 900 kPa. In all experiments, cell pressure and saturation pressure ( p) were increased incrementally in three steps to avoid damage to the sedimentary fabric. The amount of water squeezed into the specimen was measured by the volume change device. A typical pressure-water influx correlation is given in Figure F4. The progress of saturation was controlled by closing the valve to the volume change device and subsequently raising the cell pressure by up to 10%. When saturation is achieved, the ratio of pore pressure change to the cell pressure change must be >0.95. In the clayey sediments and sedimentary rocks tested, the saturation stage lasted an average of 72 hr.
p) were increased incrementally in three steps to avoid damage to the sedimentary fabric. The amount of water squeezed into the specimen was measured by the volume change device. A typical pressure-water influx correlation is given in Figure F4. The progress of saturation was controlled by closing the valve to the volume change device and subsequently raising the cell pressure by up to 10%. When saturation is achieved, the ratio of pore pressure change to the cell pressure change must be >0.95. In the clayey sediments and sedimentary rocks tested, the saturation stage lasted an average of 72 hr.
After the completion of saturation, the test specimens were consolidated. The objective of consolidation is to create a defined equilibrium and isotropic stress state before the specimen is loaded to failure. Evidently, the values of consolidation pressure are higher than saturation pressure and are always restricted by the limiting stress value of the measurement device. The pressures were chosen in intervals approximately proportional to the drilling depth of the sections (for applied consolidation pressure values see Table T1). The cell pressure was increased, starting from the final cell pressure of the saturation stage, while the formerly applied saturation pore pressure was maintained. Under these isotropic stress conditions and with open drainage, there was an initial rise in pore pressure followed by a fall due to the dewatering of the specimen into the back pressure system. When the back pressure and volume change reached a constant value with time, the consolidation stage was completed. A typical volume change-time correlation can be seen in Figure F5, which shows a graph with an initially steep slope becoming progressively flatter with time. Consolidation stages usually lasted 25-30 hr. This curve is essential for the calculation of the piston velocity of the compression stage. With the aid of the consolidation, the empirical equation (DIN 18 137, 1990, part 2; Head, 1986) gives the maximum piston velocity for drained tests:
-
max v = (h x
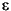 f)/(15 x t100)
f)/(15 x t100)
where
-
max v = maximum rate of deformation (mm/min);
-
h = height of sample (mm);
-
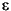 f = estimated strain at failure; and
f = estimated strain at failure; and
-
t100 = graphically constructed time at 100% consolidation (min).
The calculated rate is valid for CD tests. For CU tests, however, the rate of deformation should be at least 10 times faster. For our tests, we roughly calculated the rate then compared the latter with the order of magnitude recommended in the DIN standard (DIN 18 137, 1990) (depending on the degree of plasticity of the tested material), and, based on the results, determined a rate (Table T1). Additionally, the maximum load capacity of the triaxial testing frame (load transducer limit = 7500 N) had to be considered, so lower rates of deformation were chosen for deeper and, hence, stronger samples. In this context, it is worth mentioning the advantage of the small-diameter specimens.
To investigate if and how far clay minerals are oriented in the vicinity of the artificially induced fracture planes, small cubes of material were extracted from Sample 186-1151A-51R-1, 53-63 cm (546 meters below seafloor), in different orientations from the deformed cylinder. After freeze-drying, mounting on aluminium tables, and cathodic sputtering with carbon to make the surface of the subsamples electroconductive, the subsamples were exposed to the electron beam of the SEM. The organic matter content was determined for each tested section as the weight loss after oxidizing the material at 550°C for 2 hr (following the recommendations of DIN 18 121, 1990).

 2 =
2 =  3) are imposed by water pressure; the vertical stress (
3) are imposed by water pressure; the vertical stress ( 1) is imposed by piston load and water pressure (
1) is imposed by piston load and water pressure ( 1 = F/A +
1 = F/A +  3, with F = piston load and A = area). The water used for external and internal application of pressure to the specimen has to be de-aired to avoid measurement errors due to compressibility of the gaseous phase. The cylindrical triaxial cell encloses the specimen, which is installed on the cell base. The cell base contains the influx to and drainage off the cell and the specimen (Fig. F1). The outlets and inlets are each equipped with electrical sensors and connected through piping with either hydraulic pumps (water supply) or with measuring devices (volume change unit and pressure gauges).
3, with F = piston load and A = area). The water used for external and internal application of pressure to the specimen has to be de-aired to avoid measurement errors due to compressibility of the gaseous phase. The cylindrical triaxial cell encloses the specimen, which is installed on the cell base. The cell base contains the influx to and drainage off the cell and the specimen (Fig. F1). The outlets and inlets are each equipped with electrical sensors and connected through piping with either hydraulic pumps (water supply) or with measuring devices (volume change unit and pressure gauges).
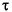 ) vs. normal stress (
) vs. normal stress ( s [1 - n])/(n
s [1 - n])/(n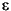 f)/(15 x t100)
f)/(15 x t100)