-
k = (K x µ)/(
x g),
The constant-flow approach measures hydraulic gradient while fluid is pumped into and out of the sample. The constant-flow permeability tests were conducted using the Trautwein Soil Testing Equipment Company's DigiFlow K (Figs. F2, F3). The equipment consists of a cell (to contain the sample and provide isostatic effective stress) and three pumps (sample top pump, sample bottom pump, and cell pump). Bladder accumulators allow deionized water in the pumps while an idealized solution of seawater (25 g NaCl and 8 g MgSO4 per liter of water) permeates the sample. ASTM (1990) designation D 5084-90 was used as a guideline for general procedures.
The retrieved Leg 201 core samples were stored in plastic core liners and sealed with wax immediately after sampling to prevent moisture loss. The sealed samples were stored in the refrigerator at 4°C until immediately prior to sample preparation. To provide freshly exposed surfaces, cores were trimmed on both ends immediately before testing using a wire saw or a utility knife, depending on core properties. After trimming the ends of the sample, the diameter and the height of the sample were measured. The Leg 201 samples had a minimum diameter of 2.3 in, and sample heights varied from 2.3 to 3.6 in. The sample was then placed in a flexible-wall membrane and fitted with filter paper and saturated porous disks on both ends. Next, the sample was placed in the cell, which was filled with deionized water so that the membrane-encased sample was completely surrounded by fluid. A small confining pressure of ~0.03 MPa (5 psi) was applied. Flow lines were flushed to remove any trapped air bubbles. After flushing the flow lines, the sample was backpressured at ~0.28 MPa (40 psi) in order to fully saturate the sample. Backpressure was achieved by concurrently ramping the cell pressure and the sample pressure to maintain a steady effective stress of 0.03 MPa. Saturation was verified by measuring the ratio of change in pore water pressure in the porous material to the change in the confining pressure (ASTM, 1990). Once the sample reached saturation, the cell fluid pressure was increased while the sample backpressure was maintained, thus increasing the effective stress on the sample. Once the target effective stress was achieved, cell pressure and backpressure were maintained. The sample was allowed to equilibrate for at least 4 hr and generally overnight (12 hr). Throughout testing, vertical sample displacement and change in cell fluid volume were monitored. The pressure difference between sample top and bottom were measured using a Validyne variable reluctance pressure transducer. The accuracy of the Validyne variable reluctance pressure transducer was ±5.2 x 10–4 MPa (±0.075 psi). All measurements and data were logged digitally in real time.
After the target effective stress level was achieved, a brief constant pressure gradient test was conducted to select an appropriate flow rate for the subsequent constant-flow tests. During the constant-flow tests, flow rates were maintained by the top and bottom pumps, one on each end of the sample, ensuring that the volume of the sample was unchanged. During the permeation step, the head gradient was monitored to ensure that gradients were not excessive (ASTM, 1990). Since fluid pressure in the closed hydraulic system was affected by temperature changes, testing was conducted within a closed cabinet with a fan to keep the internal temperature uniform. The temperature was maintained at ~30ºC (±1°C) during flow tests, and consolidation steps and temperature were monitored throughout the testing phase.
Four to five constant-flow tests were performed at each effective stress level. Once permeability values were obtained, cell pressure was increased and the sample was allowed to equilibrate overnight at the new effective stress. For every sample, four effective stress steps were performed. We used effective stress values ranging from 0.14 to 0.55 MPa. Previous permeability studies (e.g., Bolton and Maltman, 1998; Bolton et al., 2000) have shown that the largest decrease in permeability occurs as effective stress is increased from 0 to 0.1 MPa; subsequently, permeabilities remain relatively constant.
Using these measurements—the specified flow rate, Q (in cubic meters per second), and the pressure difference that was monitored by the testing equipment, hydraulic conductivity, K—values were calculated for each sample using Darcy's Law:
where
The conductivity values were then converted to permeability (k, in square meters) using the following equation:
x g),
where
= density (1020 kg/m3), and
The density value was estimated for a temperature of 30°C and a salinity of 33 kg/m3, using the equation developed by Fofonoff (1985). Assuming a reasonable water compressibility, volume change, and thus density change due to the applied pressure, is minor (<0.1%). Viscosity data were obtained from the Handbook of Chemistry and Physics (Lide, 2000) for water at a temperature of 30°C and salinity of 35 kg/m3. The average permeability was computed as the arithmetic mean of permeability values at each effective stress. The maximum pressure change during testing was 0.83 MPa (120 psi).
Uncertainties due to variations during testing were examined by determining the standard deviation of flow rates and the pressure differences in the data used to calculate permeability. The variation in flow rate was estimated in terms of standard deviation for the highest and lowest flow rates used in this study. At the highest flow rate (1.44 x 10–3 mL/s), the estimated standard deviation was 2 x 10–5 mL/s, whereas at the lowest flow rate (1.17 x 10–6 mL/s), the estimated standard deviation was 2 x 10–8 mL/s. The variation in pressure difference was estimated using a representative sample, and the standard deviation varied from 0.00069 MPa at the lowest pressure difference (0.016 MPa) to 0.0012 at the highest pressure difference (0.069 MPa).
The corresponding porosity for each estimated permeability was calculated using the change in volume of fluid (mL) contained in the cell after each consolidation step. Total sample volume (VT(0)) was calculated using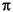 
r2h, where r is the radius of the core sample and h is the height of the sample. Initial porosities (
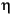0) for volume calculations were obtained from D'Hondt, Jorgensen, Miller, et al. (2003). The estimated difference between the initial porosity (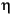0) measurements and the porosity after backpressure is, on average, ~0.5% or less. Because the change in porosity is minor, we assumed that the porosity of the sample at the end of backpressure is similar to the initial porosity (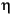0) of the sample.
Using the initial porosity (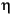0), volume of voids before the testing (Vv(0)) was calculated:
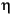0 x VT(0).
Volume of solids (Vs) was calculated using
Using the difference of cell volumes between two consecutive steps (e.g., cell volume at backpressure and cell volume at first consolidation), the change in volume of water in the cell (
VT(1)) was calculated. The new total volume of the sample (VT(1)) after pore spaces were reduced during the consolidation process was determined by subtracting the change in cell volume at the end of the consolidation step (VT(1)) from the total sample volume (VT(0)):
VT(1).
Using the calculated new total volume of the sample (VT(1)), the new porosity at the end of the consolidation was calculated. The new porosity (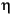1) at the end of the consolidation was
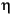1 = (1 – Vs)/VT(1).
