-
[(S1 - Pe) / (S3 - Pe)] =
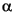 , where
, where 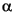 = [(1 + µ2)1/2 + µ]2, (2)
= [(1 + µ2)1/2 + µ]2, (2)
The fault and slip data extracted from the interval 820.0-880.0 mbsf were inverted in terms of stress tensor orientation and aspect ratio using a method similar to those proposed by Carey and Brunier (1974), Armijo and Cisternas (1978), Angelier (1979), and Etchecopar et al. (1981), with additional developments (Célérier, 1988, 1995; Tajima and Célérier, 1989). In all, 60% of the slip orientations can be reconciled with a N080° trending extensional stress field (Fig. 12), with S1 slightly tilted to the South and a stress ratio equal to:
S1 can be evaluated at 800 mbsf, for example, from the lithostatic charge to obtain 33.0 (± 2.0) MPa, which places bounds on the two horizontal components of the stress tensor. With a hydrostatic charge (Se) equal to about 19.0 MPa at this depth, stresses within the Alboran Sea basement might be estimated using the frictional limit of the crust proposed by Sibson (1974) or Brace and Kohlstedt (1980). A relation between maximum (S1), and minimum (S3) principal stresses and pore pressure (Pe) proposed by Jaeger and Cook (1977) was used successfully by Moos and Morin (1991), for example, as well as others. The near verticality of the borehole in the analyzed section with a deviation generally less than 7° (Fig. 7), and the S1 direction determined from active faulting (Zoback et al., 1989), establishes the validity of this model for the present analysis. The friction law is expressed as:
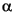 , where
, where 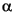 = [(1 + µ2)1/2 + µ]2, (2)
= [(1 + µ2)1/2 + µ]2, (2)
where µ is referred to as the friction coefficient.
If the pore pressure in the basement is considered to be hydrostatic (Pe = Se = 19 MPa), and S1 lithostatic (S1 = 33 MPa near the base of the hole), a simplified relationship is obtained with:
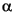 ), (3)
), (3)
and S2 can be computed from (1) and (3) accordingly.
In the lower part of the basement, the direction of the hole short-axis is found to be extremely stable in azimuth, as revealed from mechanical calipers orientation (Fig. 5, Fig. 7). The differences between the two FMS caliper readings remains, however, extremely small (under 0.1 in). This difference rarely exceeds 0.8 in (Fig. 7), except in faulted intervals (830 to 840, 860 to 870, and 900 to 910 mbsf). The process of faulting, and subsequent alteration from fluid circulation, apparently reduces locally the mechanical strength of the formation to allow for the larger size ruptures in the direct vicinity of faults (Fig. 5, Fig. 7).
Borehole wall failures leading to the development of hole ellipticity are often analyzed in terms of compressive rupture of the borehole surface (Bell and Gough, 1979; Barton, 1988; Moos and Zoback, 1990). If present in Hole 976B, which could be inferred from the stable orientation of the FMS tool in the hole and in spite of detectable ellipticity from mechanical calipers, compressive ruptures of the borehole surface must be very limited in extension. In any case, if present, these ruptures must be smaller than the size of the FMS pad (7 cm wide), although sufficient to guide the downhole sensor along more than 100 m.
While a direct determination of horizontal stress direction from hole ellipticity would here point N125° for S3, the analysis of drilling-induced faulting has previously determined a very different direction (N080°). This difference might arise from a substantial degree of mechanical anisotropy of the metamorphic rocks cored over this interval, yielding ruptures misaligned with principal stresses, as found in the KTB deep continental drilling in a geologically similar formations (Mastin et al., 1991). The slight but consistently aligned ruptures of the borehole surface from 800 mbsf to the bottom of the hole could imply that the compressive strength of the rock is here close to the limit of rupture. We may consequently equal there the maximum horizontal circumferential stress (
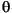
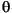 ) to the compressive strength (C0) with (Zoback et al., 1985):
) to the compressive strength (C0) with (Zoback et al., 1985):
The knowledge of C0 may then lead to another evaluation of S2 and S3 (Moos and Morin, 1991) as a function of µ, combining equations (1), (2), and (4). C0 may also be estimated from (3) and (4) with:
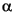 )]. (5)
)]. (5)
leading to a very narrow range of values for C0 (25.8 to 27.3 MPa; Fig. 13) over a wide range of friction coefficients (µ). The values of µ under 0.40-0.50 would correspond to the presence of very weak faults. The large number of extensional to strike-slip ruptures mapped from acoustic images advocates here for a very low difference between components of the stress field, hence from Figure 13 for the lower range of values of friction coefficient (µ) where differential stresses are lower.