- A(t) = Ao
[1 -
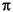 ft/Qn]n,
(1)
ft/Qn]n,
(1)
Methane in deep-sea sediments can take the form of a solid hydrate as well as free gas, two forms with physical properties significantly different from each other as well as from the fine-grained muds of the Blake Ridge in which the hydrate is found (Fig. 1). For this reason we are able to quantify the presence of methane through seismic methods, namely through the measurement of acoustic or compressional velocity (Vp), shear velocity (Vs), and quality factor (Q) or inverse of effective attenuation. Measurements of Vp in the hydrate stability zone (HSZ), and underlying gas stability zone (GSZ) of the Blake Ridge have been made using multichannel seismic reflection data (Paull and Dillon, 1981; Rowe and Gettrust, 1993; Wood et al. 1994), wide-angle, ocean-bottom hydrophone data (Katzman et al., 1994; Korenaga et al., 1997), and most recently vertical seismic profiles (VSPs) acquired on Ocean Drilling Program (ODP) Leg 164 (Holbrook et al., 1996; Pecher et al., 1997, and unpubl. data). Although Vp is quite useful for delineating the regions of gas below the HSZ, only moderate success has been achieved at quantifying small amounts of hydrate within the HSZ, (Holbrook et al., 1996). If the hydrate acts as a cement (Dvorkin and Nur, 1993), then Vs and Q may be quite sensitive to small amounts of hydrate. Pecher et al. (1997) have reported an intriguing high Vs layer in the HSZ, but to date thorough analyses for Q in this area have not been widely reported.
We used two independent data sets in this study, a single-channel seismic (SCS) reflection profile acquired as part of a site survey for Leg 164 (Line 31, Katzman et al., 1994), which passes over Sites 994, 995, and 997, and vertical seismic profiles acquired with air- and water-gun sources at Site 995. The SCS source was a 160-in3 dual chamber air-gun, with minimal bubble pulse and a wide band (20-150 Hz at 20 dB down from the peak). The VSPs on Leg 164 were acquired with a 300-in3 Bolt model PAR 1500 air-gun, suspended 5 m from the sea surface, and a 400-in3 Seismic Systems model P400 pneumatic water-gun suspended 4 m from the sea surface. The source signatures and spectra are shown in Figure 2, revealing the compact broad band nature of the air-gun source used in the SCS profile.
The SCS line analyzed, Line 31 from Katzman et al. (1994), is displayed in Figure 3A after application of a time shift to make the seafloor horizontal. An alternative means of displaying the data is to plot at each time sample a frequency that is representative of the amplitude spectrum for a portion of the trace windowed about that sample. The representative frequency used here is the centroid frequency. This is computed by first determining the area of the frequency domain amplitude spectrum for the windowed portion that lies above the noise. The noise level for this calculation was assumed to be 0.1 of the peak value, or 20 dB down. The centroid frequency is that frequency which divides the area of the amplitude spectrum above the noise into two equal area portions. The result of this operation is the spectrogram shown in Figure 3B. Because migration can distort frequency spectra, the spectrogram was computed using unmigrated data. The time window used to compute the frequencies was a 64 sample cosine tapered window. To laterally smooth the result, the spectra from four adjacent traces were stacked before centroid frequency computation. It is quite apparent from this display that the data are sensitive to frequency content (note the sharp drop below the BSR), and that a quantitative analysis of this effect may at least allow detection, and possibly quantification, of hydrate and gas. With this objective, a nonlinear inversion for attenuation based on spectral modeling was applied to the data.
To implement the inversion, we use the operational definition of attenuation given by Aki and Richards, (1980),
where A(t) is the amplitude of the seismic signal of frequency f, after traveling for a length of time t, and number of cycles n, through a medium with a quality factor of Q, and with a starting amplitude Ao = [A(t = 0)]. Note that Q and attenuation are inversely related. Because we may want to analyze layers that are less than a few cycles thick, we retain this exact form of the equation above in favor of the more common approximate form for many cycles, which involves an exponential (Aki and Richards, 1980).
Mechanisms for intrinsic Q (absorption) include grain sliding, viscous flow of pore fluid (or gas), and perhaps viscous relaxation (Stoll and Bryan, 1970; Johnston et al., 1979). Another phenomenon, scattering, as from intrabed multiples, has nearly the same effect as intrinsic Q and can be included with the intrinsic Q into an inclusive effective Q. Schoenberger and Levin (1974, 1978) and Kang and McMechan (1994) have found independently that 20%-80% of the effective attenuation may be attributable to either phenomenon, depending on the geological model. In this study we measure effective Q, so both mechanisms must be included in the interpretation of the results. We also assume here that Q is frequency independent (implying a dispersionless medium), which is a reasonable assumption at these frequencies (Murphy, 1982; Bowles, 1997).
To determine the magnitude of a possible Q anomaly due to hydrate or gas, we must first determine what Q should be expected from hydrate-free sediments. Although the bulk of field and lab studies reported in the geophysics literature regarding attenuation have been performed on sands, Bowles (1997) recently compiled an extensive list of compressional wave attenuation studies that have been performed on fully saturated fine-grained marine sediments. The results were originally reported in units of dB/m and were converted to Q for comparison here using a velocity of 1600 m/s. For frequencies between 20 and 250 Hz, reported Q for the silts and clays covered a very large range, from 60 to 2500. Most of the values are concentrated between 200 and 700. These values are similar to Q values obtained through analysis of VSP data in Texas by Hauge (1981), who reported Q as high as ~500 for shales in the Gulf of Mexico. There does not seem to be a significant modal character to the data (suggesting different attenuations for hydrate-bearing sediment), nor was the presence of hydrate reported. We therefore assume a reasonable Q for nonhydrate-bearing sediment to be ~400.
There exist very few quantitative reports of Q in gas sands, and even fewer in gassy mud. Some of the lowest Q values reported for fine-grained marine sediments (Q = 50-60; Hamilton, 1976; Bowles, 1997) may have unknowingly incorporated some gas, but they were not reported as gas bearing. Using sandstones, Murphy (1982) measured Q over a range of partial saturations and frequencies, and showed at 100 Hz a decrease in Q from 50 at 100% saturation to 22 at 90% saturation and back to 50 as saturation decreases. This rather interesting local minimum of Q at partial saturation was attributed to peak loss of energy from pore fluids moving relative to the surrounding matrix. Others report similar values (Q ranging between 10 and 100) for dry, as well as saturated sandstones in the lab (Toksoz et al., 1979; Frisillo and Stewart, 1980) and unconsolidated sediments in the field (Badri and Mooney, 1987). We therefore expect Q for gassy muds to be between 10 and 100.
For hydrate-bearing sediments, we expect a higher Q than for hydrate-free sediments, analogous to frozen vs. unfrozen sediments, (Toksoz et al., 1979). Perhaps the best estimate of Q through hydrate-bearing sediment comes from Brienzo (1992), who made no mention of hydrate, but reported somewhat high values of Q, ranging from 660 at the seafloor to 175 at 750 mbsf in the Monterey deep-sea fan, a thick sediment column in 2800 m of water where hydrates are very likely to be found. This value is consistent with the higher Q values reported by Bowles (1997), which may also have been unknowingly acquired in hydrate-bearing sediments. Although Jacobson et al. (1981) also reports Q from deep water (~3000 m in the Bay of Bengal), the values are generally between 50 and 200. Based on these reports, our a priori estimates of Q are 200-700 in the HSZ and Q = 10-100 in the GSZ.