DATA RESOURCES AND METHODS
In the following chapter, the maximum drill depth of 367 mbsf reached in Hole 1103A is divided into three depth ranges: 0-70, 70-244, and 244-367 mbsf. Each depth interval is discussed separately regarding available velocity information and processing techniques used.
The depth interval between 0 and 70 mbsf is particularly limited with regard to available velocity information and, thus, is the most speculative one. Unstable hole conditions caused the pipe to be pulled up only to 84 mbsf prior to logging. No useful logging data were obtained through the pipe over the first 75 m. Very low core recovery in this interval also prevented the collection of velocity data in the laboratory. Based on laboratory measurements on core samples recovered from Hole 1100C of the shelf transect, we measured reasonable shipboard Hamilton frame (PWS3 contact probe system) values of 1650-1700 m/s for the upper 0-3.5 mbsf (Shipboard Scientific Party, 1999b). In order to fill the remaining gap from 3.5 to 75 mbsf, all available Ocean Drilling Program (ODP) and Deep Sea Drilling Project (DSDP) velocity information was compiled from Antarctic shelf topsets (Fig. F2). For this study, we considered data of four existing drill sites depending on the availability of data, shelf geometry, location on the shelf, and reported lithology: Site 739 of ODP Leg 119 in Prydz Bay and Sites 270-272 of DSDP Leg 28 in the Ross Sea. Of all recorded shelf topset values between 5 and 75 mbsf, 92% are in the range of 1800 to 2500 m/s. The average of all recorded velocity values over this depth interval is 2172 m/s. Considering sediment descriptions and corresponding logging data given in the Leg 119 Initial Reports volume (Shipboard Scientific Party, 1989) and by Hambrey et al. (1991), sediments from Site 739 consist of dominantly uncemented diatom-rich diamictites with large igneous and metamorphic clasts in the upper 70 mbsf. Even though the degree of compaction may differ compared to sediments of the upper 70 mbsf of Site 1103, Leg 178, the recorded velocities are close to the overall topset values considered in our comparison (2112 m/s).
In summary, we took three velocity values from Site 1100C of the shelf transect in the depth range of 0.7-3.5 mbsf and added a velocity value of 1630 m/s at the sediment/water interface (0 mbsf). The seafloor value of 1630 m/s is based on extrapolations of the Site 1100C data mainly for ease of use in later calculations of depth-traveltime curves and synthetic seismograms. For the following interval between 3.5 and 70 mbsf, we used the average velocity (2112 m/s) of Site 739 (5-75 mbsf), ODP Leg 119, Prydz Bay. In addition to geological reasons, the decision to take Site 739 velocity values is based on the availability of logging data and the good agreement between logging and laboratory derived data for this site. Considering the introduced error, the assumptions are reasonably conservative because all known mid-shelf Antarctic velocities of the upper 75 mbsf only show small acoustic velocity variations focused in the 1800 to 2500 m/s range.
Three logging tool strings (triple combination [TC], geological high-resolution magnetic tool [GHMT], and the Formation MicroScanner [FMS]-sonic tool]) were deployed at Hole 1103A. After completion of the TC logging descent, difficulties in reentering the base of the pipe resulted in the loss of the 1.5-m-long accelerator porosity sonde (APS) bow spring. In order to avoid complications with the missing parts still in the borehole, the FMS-sonic tool was used without its three centralizing bow springs of the mechanical caliper device (MCD) (Fig. F3). During two logging passes with the FMS-sonic tool (Fig. F3), transit-time and velocity information were obtained between 124 and 244 mbsf (during the first run, pass one) and from the seafloor to 243 mbsf (during the second run, pass two).
The Schlumberger sonic logging tool used at Site 1103A is commercially known as the array sonic or sonic digital tool (SDT) (Fig. F4). It carries two piezoelectric ceramic monopole transmitters that are separated by 2 ft near the downhole end of the tool. The transmitted signals have a dominant frequency of 10 kHz with a fire rate of 7.5 Hz. Ten ceramic receivers are arranged at various spacings uphole with respect to the transmitters. Two of the receivers are located in the central part of the tool, at distances of 3 and 5 ft from the upper transmitter. The remaining eight wideband receivers are clustered 6 in apart, forming an array near the top of the tool from 8 to 11.5 ft above the upper transmitter (Schlumberger, 1989). The various transmitter/receiver spacings allow the simultaneous recording of many different transit times. Detection and recording of an "analog transit time" occur in each case when the signal level at the receiver crosses a fixed threshold. This may or may not occur on the true first arrival of the signal, depending on several circumstances impacting the signal-to-noise ratio downhole. The standard output transit times with their respective transmitter/receiver spacings are listed in Table T1. A graphic representation is given in Figure F4.
Four differential time or  T outputs of the logging software (Delta-T [DT] computed from TT1, TT2, and TT4; Delta-T Long [DTL] computed from TT1, TT3, and TT4; Delta-T Long Near [DTLN] computed from LTT1, LTT2, and LTT4; and Delta-T Long Far [DTLF] computed from LTT1, LTT3, and LTT4) estimate the formation slowness (inverse of velocity). Each relies on a computation combining four individual transit-time outputs. This gives an answer that is compensated against small inaccuracies resulting from tool tilt, sudden changes in hole diameter, etc. However, should a single transit time be detected incorrectly, any DT output that uses it is rendered completely invalid.
T outputs of the logging software (Delta-T [DT] computed from TT1, TT2, and TT4; Delta-T Long [DTL] computed from TT1, TT3, and TT4; Delta-T Long Near [DTLN] computed from LTT1, LTT2, and LTT4; and Delta-T Long Far [DTLF] computed from LTT1, LTT3, and LTT4) estimate the formation slowness (inverse of velocity). Each relies on a computation combining four individual transit-time outputs. This gives an answer that is compensated against small inaccuracies resulting from tool tilt, sudden changes in hole diameter, etc. However, should a single transit time be detected incorrectly, any DT output that uses it is rendered completely invalid.
Nowhere in the logged interval were all transit times simultaneously correct. Typically, four or five of the eight were wrong at any given depth, rendering the standard formation slowness estimates completely useless. There are several reasons why this might have occurred. In general, large boreholes (>13 in) and unconsolidated formations are challenging for sonic logging because the signal is attenuated by travel through fluid and slow formation. The fundamental problem with slow formations (<2000 m/s) and the high firing frequency of 10 kHz is the resulting long wavelength with the possibility of interference of subsequent wavelets at the receivers. Additionally, the lack of the upper centralizing unit (MCD; Fig. F3) resulted in the tool being off center, further attenuating the signal and causing additional acoustic noise generated by the tool touching the borehole wall. Consequently, the automatic detection of the signals received at the array and at the two other receivers was inconsistent over time, and the signal was often picked within noise preceding the first true arrival (Shipboard Scientific Party, 1999b). Another reason for the recording of poor and inconsistent data could be due to strong velocity inhomogeneity within the logged formations. Tills with unlithified matrix and large clasts show large velocity differences within the measurement range of the tool. Matrix velocities may be in the range of 1800 m/s, whereas those of crystalline clasts can be as high as 5000 m/s (e.g., fig. 24 and PWS3 data for Site 1103 in Shipboard Scientific Party, 1999b). Judging from FMS image observation, large clasts of different sizes, embedded in a finer grained matrix, are unequally distributed around the borehole. Therefore, it seems possible that an emitted signal can take strongly contrasting travel paths on different sides of the borehole wall.
An additional DT output of the logging software (referred to herein as DC) is calculated using digital coherence mapping. At each 6-in (~0.15 m) sample interval, the waveforms of the eight wideband array receivers are digitized and stacked with various time offsets that compensate for moveout. The correct moveout (and formation slowness) at each depth is recognized from the offset that produces the highest amplitude stack. The data obtained are self diagnostic to some degree in that the coherency of the eight waveforms is a quantifiable indicator of confidence in the data. This technique is more robust in the difficult conditions described above, but in this case, only limited intervals featured coherent waveforms. Small-scale formation inhomogeneity may have contributed to the lack of a consistent moveout across the 3.5-ft array.
Remedial onboard processing focused individually on the widely spaced receiver/transmitter geometries LTT1 (10 ft) and LTT2 (8 ft) that showed the most consistent transit times. But this is a weak technique, considering that individual transit times do not account for traveltime within the drill slurry gap between tool and formation. A first attempt toward determining true formation velocities was to divide the transit time by the transmitter-receiver spacing and to add 10% to the resulting velocity to correct for the acoustically slower gap between tool and formation (Shipboard Scientific Party, 1999b). This method is not capable of correcting for varying borehole diameters and varying densities of the slurry within the tool/borehole gap. Additionally, the method assumes that a signal recorded in acoustically faster formations will also pass the tool/borehole gap faster than a signal recorded within acoustically slower formations. These data also have inherently poor vertical resolution determined by the transmitter-receiver spacing used.
In contrast, the data processed postcruise and presented in this paper uses exclusively differential times ( T), which automatically account for the tool-formation gap. Any pair of transit times of different spacing can be used to estimate formation slowness, provided that they are of different transmitter-receiver spacings. Dividing the difference in transit time by the difference in transmitter-receiver spacing, we obtain a
T), which automatically account for the tool-formation gap. Any pair of transit times of different spacing can be used to estimate formation slowness, provided that they are of different transmitter-receiver spacings. Dividing the difference in transit time by the difference in transmitter-receiver spacing, we obtain a  T:
T:
-
 T = (TTA-TTB)/(TRSA-TRSB), (1)
T = (TTA-TTB)/(TRSA-TRSB), (1)
where
-
 T = differential traveltime,
T = differential traveltime,
-
TTA = traveltime of transmitter A,
-
TTB = traveltime of transmitter B,
-
TRSA = transmitter-receiver spacing A, and
-
TRSB = transmitter-receiver spacing B.
The pitfall of this method is that all errors in transit-time detection result in large velocity errors and only small sections of the record, therefore, contain useful velocity information. Our method is less elegant than Schlumberger's default computation, which uses four transit times per  T; however, by relying on only two transit times simultaneously, we greatly improved our chance of obtaining valid slowness/velocity data. In order to discern these valuable velocity data, we compared results of one processing technique using data from the two different logging passes or compared the results of the same pass achieved with different techniques.
T; however, by relying on only two transit times simultaneously, we greatly improved our chance of obtaining valid slowness/velocity data. In order to discern these valuable velocity data, we compared results of one processing technique using data from the two different logging passes or compared the results of the same pass achieved with different techniques.
Two of the total of 13 incorporated data categories and processing techniques described below are subject to human judgement and experience. Some of the data categories use information twice—all of those instances are noted.
Logging Velocity Data Categories
In this section we briefly introduce and discuss the different data categories. To make the chosen abbreviation for the data categories more transparent, two examples are given. The data category "AFA2/1(LTT1 + 2) match av" is composed of "AFA," for analog first arrival, "2/1" comparing pass one and two of transmitter receiver spacing "LTT1" and "LTT2." The additional abbreviation "match av" indicates that matching velocity values of both passes of the same depth have been used to calculate a mean or average value (av) representative for this data category and depth. Data category "2DC2a/DC2 match av" for example is based on velocity values obtained by digital coherency mapping (DC) of wavelets collected during run 2. The abbreviation "a" indicates special processing parameters, explained in detail in the section of the "DC2a/DC2 match av" data category. The abbreviation "match av" again indicates that matching velocity values of both processing types (DC2a and DC2) of the same depth have been used to calculate a mean value representative for this data category and depth.
AFA2/1(LTT1 + 2) Match Av
This category uses transit times LTT1 (10-ft spacing) and LTT2 (8-ft spacing). Calculated velocities of the first and second passes are compared. Using a 300 m/s quality criteria, all data that exceed this velocity difference are excluded from passes one and two. Data within this range are included using an average velocity of the first and second passes. Long-spaced transmitter and receiver pairs may be favorable in lithologic units with strong velocity inhomogeneities within the depth resolution of the tool because they integrate over a larger rock volume.
AFA1(LTT1 + 2) and AFA2(LTT1 + 2) Picked by Log Character
This graphical method uses the two transit-time plots of the two receiver/transmitter pairs LTT1 and LTT2 and the resulting velocity plot of each pass without comparing the two passes with each other and without looking at absolute velocity values. We believe that the DT calculated from these two transit times merits special attention; of all the transit times recorded, LTT1 and LTT2 performed best. This is based on the subjective experience of the logging engineer, observation of the waveforms during acquisition, and log quality control standards set forth by Schlumberger (Bateman, 1985). Admitting that this method is largely subjective, it is nevertheless an independent approach to extract useful data. The major advantage of this method compared to the previous category (AFA2/1[LTT1 + 2] match av) is that it is entirely focused on repeatability. Tool position, noise level, and a number of other variables can cause differences in quality and lack of repeatability between passes. In this category, valuable information from one pass that has no counterpart in the other pass can be included.
AFA1(LTT1, -2, -3, -4; TT1, -2, -3, -4) and AFA1(LTT1, -2, -3, -4; TT1, -2, -3, -4) High, and AFA2(LTT1, -2, -3, -4) and AFA2(LTT1, -2, -3, -4) High
These data categories are the result of an unusual statistic and combinatorial processing approach. We computed differential transit times for all available transmitter and receiver spacings (LTT1, -2, -3, and -4; and TT1, -2, -3, and -4). For N number of initial transit times it is possible to generate q number of combinations:
-
q =
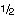 (N2 - N). (2)
(N2 - N). (2)
Using all recorded transit times with their respective geometries, besides the six values of the wideband receiver array (Fig. F4), there are 28 possible and 26 actual resulting velocities for the first pass, as two transmitter/receiver pairs have the same spacing (LTT1/LTT4 and TT1/TT4). Unfortunately, TT1, -2, -3, and -4 transit times were not recorded for the second logging pass. Consequently, only five velocity combinations are possible. The resulting velocities for each pass were then compared (Eq. 2), leading to 325 combinations for the first pass and 10 combinations for the second pass. The confidence level was again 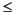 300 m/s difference in velocity. Additionally, all average resulting velocities <1500 m/s (water velocity) and >6000 m/s have been excluded.
300 m/s difference in velocity. Additionally, all average resulting velocities <1500 m/s (water velocity) and >6000 m/s have been excluded.
For logging pass two, with 10 possible average velocities for each depth interval, the values were mostly within a narrow range and a simple average was calculated as a result for this pass and category. In the case of two distinct populations, the higher value in the AFA2(LTT1, -2, -3, -4) high category was saved. Only 159 out of 1050 possible values in the depth interval 85-243 mbsf met the criteria.
For logging pass one, with 325 possible average velocities for each depth interval, up to 117 actual values were received using the 300 m/s confidence interval and the plausibility range of 1500-6000 m/s. As a guide for decision making, the values of the first pass were sorted in descending order, and small graphs were plotted for most of the depth intervals (Fig. F5). Four cases are common. Typically, the values have a stable plateau at the high-velocity side (Fig. F5A) and only some anomalies at the low side of the values. The choice of high velocities for a final value for this depth interval and category is based on the observation that analog picking in noisy, highly attenuated signals of our log commonly resulted in velocities lower than those expected. Additionally, all signals that travel only through drill slurry will produce lower velocities. However, at several depth intervals, erratic velocities were also observed at the high end of the velocity spectrum (Fig. F5B). These values may be the result of cable noise, malfunctioning transducers, or waves traveling alongside the tool. In both cases (Fig. F5A, F5B), the erratic values are relatively easy to detect. Their numbers are commonly small compared to the population of reasonable values, and usually the erratic values differ significantly from the majority of the values for the same depth interval and values of preceding and subsequent depth intervals. Since the aperture of measurement with this technique (equal to the distance between the two receivers used) is between 2 and 9 ft, abrupt changes in measured velocity from one 6-in depth interval to another are unlikely, even if the geological profile contains sudden major impedance changes. During the semiautomatic sorting and evaluation of the values, depth intervals with two distinct bimodal velocity populations were also evident (Fig. F5C). Because decisions are likely to be biased in those instances, the higher values were included in a separate category (AFA1[LTT1, -2, -3, -4; TT1, -2, -3, -4] high), similar to the high values of the second logging pass. A total of 751 out of 793 possible values in the depth interval 124-244 m meet the criteria for category AFA1(LTT1, -2, -3, -4; TT1, -2, -3, -4). Nonconclusive velocities were found for 5% of the depth intervals for this category and pass.
AFA1/2(LTT1, -2, -3, -4; TT1, -2, -3, -4) Match Av
This category compares values of the previous categories AFA1(LTT1, -2, -3, -4; TT1, -2, -3, -4) and AFA2(LTT1, -2, -3, -4). The average of velocity values of the same depth interval with a difference of 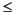 300 m/s between the first and second pass were incorporated. Although this category introduces data twice into the initial data pool without utilizing new processing aspects, it seemed especially important to emphasize agreeing results of the first and second pass. More than 80% of the few values (112) in the depth interval 124-243 mbsf found in pass one (category AFA2[LTT1, -2, -3, -4]) matched their depth counterparts in logging pass two (category AFA1[LTT1, -2, -3, -4; TT1, -2, -3, -4]).
300 m/s between the first and second pass were incorporated. Although this category introduces data twice into the initial data pool without utilizing new processing aspects, it seemed especially important to emphasize agreeing results of the first and second pass. More than 80% of the few values (112) in the depth interval 124-243 mbsf found in pass one (category AFA2[LTT1, -2, -3, -4]) matched their depth counterparts in logging pass two (category AFA1[LTT1, -2, -3, -4; TT1, -2, -3, -4]).
DC1/2 Match Av
Digital coherency mapping output is based on the eight digitized wavelets received at the wideband receiver array (Fig. F4) as described above. In depth intervals with low coherency and disturbed signals, the coherency mapping technique has a tendency to produce significantly higher velocities than the velocities derived by analog picking. The category DC1/2 match av contains average velocity values of the first and second pass (see Fig. F6 for an example of data of the second logging run) calculated from values with a difference of 300 m/s or less for a specific depth interval. Of the 783 velocities acquired in both logging runs for the same depth intervals, 518 meet the 300 m/s criteria (66%).
DC2 High Coherency
This category represents velocity values derived by coherency mapping of the recorded wideband receiver array of the second logging pass. Only depth intervals with excellent coherency values, indicating stable receiver signals, were included. This category may contain information that has already been used within the previous category. Nevertheless, it is important to regard additional valuable data which is only present within the second pass. Of the 1599 velocity values (depth interval 0-243 mbsf) acquired in logging run two, only 270 meet the high coherency criteria (~17%).
DC2a/DC2 Match Av, DC2a/DC1 Match Av
The digital coherency mapping and subsequent tracking of coherent velocities across a certain depth interval is dependent on user-defined boundary parameters. For DC2a processing, we limited the portion of the waveform included in each stack with respect to the moveout applied. The aim was to filter out spurious coherency peaks that might be due to the arrival of slow compressional waves traveling strictly through a single medium (either the slurry or the tool housing). The resulting velocities are compared with the velocities from the DC1 and DC2 processing. Again, averages are calculated for velocities with a difference of 300 m/s or less. We introduced 1242 velocity values (78%) from data category "DC2a/DC2" and only 450 (57% out of 783) from category "DC2a/DC1 match av" to the final data pool. The high quantity of data introduced from category "DC2a/DC2" into the data pool, is based on the fact that category "DC2a/DC2 match av" contains velocity comparisons of the same original data and logging run with only modified recalculation parameters for the digital coherency mapping.
Pipe Values 0-84 mbsf, (DC2, DC2a/DC2 Match Av, AFA2[LTT1, -2, -3, -4])
Acoustic data recorded within the drill pipe may carry no, or only limited, information concerning the geological formation. Numerous wave types with different transit times occur in closed forms with a low velocity center (e.g., love, raleigh, and tube waves) (Dresen, 1985). In general, the data should be neglected or treated with extraordinary care. Only a few recorded pipe values are incorporated into the data pool (Fig. F7).
During different coherency mapping approaches and statistical analog-picked analyses (AFA2[LTT1, -2, -3, -4]), several velocity classes were observed. Three of these will be mentioned here. Velocities around 1600 m/s are probable from signals traveling within the water and mudfilled gap between tool and pipe. Velocities around 3500 m/s may result from waves that travel along the pipe/water interface (refraction waves). Some processing categories show values around 2250 m/s. Those values are close to the suspected formation velocity and also occur in the statistically treated category AFA1(LTT1, -2, -3, -4).
However, we rejected most of the pipe data and included only about 9 m (75-84 mbsf) into our data pool. Within this depth range, the pipe data are in good agreement with laboratory determined velocitie.
Below the S1/S3 (Fig. F1) unconformity, core recovery improved from 2.3% to 34% because of a change in matrix induration. We measured laboratory compressional wave velocity data aboard ship using the PWS3 contact probe system for specimens and split cores. (Shipboard Scientific Party, 1999b, fig. 24 and PWS3 data for Site 1103).
Preliminary comparisons of velocity data and lithologic descriptions (Eyles et al., 2001) suggest that all recovered lithologic changes are represented within the velocity data measured. We still have no information for 60% of the core. In order to produce a continuous velocity log for subsequent users, the following assumptions were made based on the available data. Considering the laboratory velocity and density data (Shipboard Scientific Party, 1999b), low-recovery zones are commonly located at acoustic impedance changes. We, therefore, assume that all major impedance changes are represented within the available data. Furthermore, in order to reduce data gaps by two-thirds of their depth interval, we added artificial data points at both ends of the gap. This measure is supported by the observation of discrete changes in sedimentology within the cores recovered (interchange of clast rich structureless diamictite with more sorted sands and silts). Using a simple interpolation technique to fill the data gaps would have caused unrealistic continuous transitions within the velocity profile that are also nonpreferable for later seismic modeling (e.g. synthetic seismograms).

 T outputs of the logging software (Delta-T [DT] computed from TT1, TT2, and TT4; Delta-T Long [DTL] computed from TT1, TT3, and TT4; Delta-T Long Near [DTLN] computed from LTT1, LTT2, and LTT4; and Delta-T Long Far [DTLF] computed from LTT1, LTT3, and LTT4) estimate the formation slowness (inverse of velocity). Each relies on a computation combining four individual transit-time outputs. This gives an answer that is compensated against small inaccuracies resulting from tool tilt, sudden changes in hole diameter, etc. However, should a single transit time be detected incorrectly, any DT output that uses it is rendered completely invalid.
T outputs of the logging software (Delta-T [DT] computed from TT1, TT2, and TT4; Delta-T Long [DTL] computed from TT1, TT3, and TT4; Delta-T Long Near [DTLN] computed from LTT1, LTT2, and LTT4; and Delta-T Long Far [DTLF] computed from LTT1, LTT3, and LTT4) estimate the formation slowness (inverse of velocity). Each relies on a computation combining four individual transit-time outputs. This gives an answer that is compensated against small inaccuracies resulting from tool tilt, sudden changes in hole diameter, etc. However, should a single transit time be detected incorrectly, any DT output that uses it is rendered completely invalid.
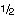 (N2 - N). (2)
(N2 - N). (2)
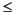 300 m/s difference in velocity. Additionally, all average resulting velocities <1500 m/s (water velocity) and >6000 m/s have been excluded.
300 m/s difference in velocity. Additionally, all average resulting velocities <1500 m/s (water velocity) and >6000 m/s have been excluded.