PALEOMAGNETIC DATA AND ANALYSIS
A variety of rock types, sample sizes, magnetometers, and demagnetization techniques were used in this study. Each data type has strengths and weaknesses, which when recognized can be used to obtain accurate paleomagnetic estimates within the uncertainty bounds. In this section, we outline the laboratory methods used to obtain the raw paleomagnetic observations and the analysis methods used for estimating paleolatitudes.
We also provide a complete archive of the data in ASCII format. The data include shipboard split-core data that are available through ODP, but were not archived in the Leg 165
Initial Reports volume, as well as data collected since Leg 165. Table 2 lists the contents of the
ASCII tables (Tables 3-18).
Long-Core Results from Shipboard Measurements
The laboratory methods and results of shipboard paleomagnetic measurements are described in detail in Sigurdsson, Leckie, Acton, et al. (1997). Briefly, we measured the remanent magnetization of archive-half sections (split cores) with a 2G Enterprises 760R long-core magnetometer
(Table 3, Table
4, Table 5, Table
6, Table 7, Table
8, Table 9, Table
10). Typically, measurements were made every 5 cm prior to and after alternating field (AF) demagnetization. AF demagnetization steps were typically 0, 10, and 20 mT, although occasionally the 10 mT step was skipped owing to time constraints and occasionally 5, 15, or 25 mT demagnetization was used. Never did demagnetization exceed 25 mT because of the limits of the AF coils.
Many of the data from the long-core magnetometer probably contain valid estimates of the characteristic remanence (ChRM) of the sediment. Unfortunately, assessing which intervals are accurate recorders is not easy given the small number of demagnetization steps, the small size of the highest demagnetization step used, the low magnetization of some intervals, coring disturbance, and the ubiquitous presence of a steep downward-directed drill-string overprint.
The overprint is by far the biggest obstacle, though it is probably wholly or at least mostly removed by 10-30 mT demagnetization. This level of demagnetization, however, further reduces the magnetization of the core, with the magnetization of many intervals reaching the resolution of the magnetometer (~2 x 10-4 A/m for a split core). Other intervals apparently do not record a ChRM, the ChRM has been destroyed by diagenesis, and/or the sediments are void of magnetic minerals, in some cases so much so as to be diamagnetic (e.g., Site 1000; Sigurdsson, Leckie, Acton, et al., pp. 251-252, 1997).
We attempted to obtain estimates of the ChRM from the split-core data of the sediments and sedimentary rocks by devising several criteria intended to avoid overprinted or magnetically unstable intervals. Our criteria included (1) rejecting any results below 10-mT demagnetization, (2) rejecting any interval with inclinations steeper than ±60°, a very likely sign that the drill-string overprint is present, (3) rejecting weakly magnetized intervals (<2 x 10-4 A/m), and (4) requiring that directions following two or more AF demagnetization steps of 10 mT or higher from the same interval differ by <3° (a weak analogy to principal component analysis). We also used progressive demagnetization experiments from discrete samples to assess whether an accurate ChRM estimate could be obtained at demagnetization of 10-25 mT
(Fig. 2, Fig.
3, Fig. 4). In some cases, obtaining an accurate estimate of the ChRM was difficult even for demagnetization up to 70 mT
(Fig. 2). In general, the demagnetization experiments showed that for most intervals 20 mT was marginally sufficient to remove the drill-string overprint
(Fig. 3, Fig.
4), but in some intervals up to 25-30 mT was required (Fig.
3).
For the split cores from sedimentary units, the number of demagnetization steps completed during Leg 165 were so few that only a few intervals pass the above criteria. Furthermore, demagnetization rarely exceeded 20 mT for the sedimentary cores, which is about the minimum AF field needed to remove the drill-string overprint. Thus, although split-core results for sediments and sedimentary rocks hint at the true ChRM inclinations, significant biases and large uncertainties remain that do not permit their use for paleolatitude estimates. Had the split cores been demagnetized at more steps with higher peak fields (25-70 mT), they very likely could have contributed significant information.
The split-core data from basalt cores, however, provide accurate estimates of the ChRM inclinations for several reasons. Mainly, the results from the basalt cores differ from those from the sedimentary cores because the magnetization of the basalts is much stronger and the overprint is removed by ~10-20 mT, as has been confirmed by the detailed demagnetization of both split-core and discrete samples (e.g.,
Fig. 5; also see Table
14, Table 18). The agreement between the split-core and discrete inclinations from similar intervals, as well as the agreement between split-core inclinations from Holes 1001A and 1001B, are further indication of the quality of the split-core results
(Fig. 6).
Because all the basalt cores were demagnetized at 20 mT and most at 25 mT, we have continuous results downcore at demagnetization levels sufficient to resolve the ChRM inclination
(Table 15). The continuity of the split-core data is important in that the number of discrete samples collected are, by themselves, insufficient to cover the basalt cores at the same resolution as the split-core data. The higher resolution of the split-core data is particularly useful in assessing the independence of stratigraphically adjacent flow units in sampling geomagnetic SV.
Discrete Samples from Shipboard and Shore-Based Measurements
Discrete samples are either 6-cm3 cubes collected in 2 cm x 2 cm x 1.5 cm plastic boxes or 8- to 12-cm3 minicores with a 2.5-cm diameter. These samples were measured at several different laboratories (University of New Mexico, Texas A&M University; Université Pierre et Marie Curie; and on the JOIDES Resolution using the Molspin magnetometer during Leg 165 and using a new 2G Enterprises cryogenic magnetometer during Leg 178) and were subjected to a variety of AF and thermal demagnetization treatments
(Table 11, Table
12, Table 13, Table
14). For samples that gave linear demagnetization paths on vector demagnetization diagrams, principal component analysis (PCA) (Kirschvink, 1980) was applied to the demagnetization results to determine the ChRM. The Maximum Angular Deviation (MAD) angle, a measure of how well the demagnetization data fit a line, was used to reject samples that gave poorly resolved directions. The MAD angle was required to be <10°, and we generally did not require that the demagnetization paths pass through the origin of the demagnetization plot in the PCA analysis (the "free" option of standard paleomagnetic PCA;
Table 16, Table
17, Table 18). Only samples with inclinations between +60° and -60° were used. Inclinations steeper than this were rare except in some of the youngest unconsolidated sediments that were weakly magnetized, and, therefore, whose primary magnetizations were likely swamped by the steep drill-string overprint.
Averaging Geomagnetic Secular Variation
Sedimentation rates are lower than 50 m/m.y. (5 cm/k.y.) for Sites 998-1001, typically averaging between 10 and 20 m/m.y. Each sample from a sedimentary unit therefore includes sediments that were deposited over several hundred years to ~2000 yr. To completely average geomagnetic SV, samples spanning a time interval of ~105-106 yr (more than ~2 m of sedimentary section on average, and <50 m assuming the highest sedimentation rates) are considered sufficient to average SV. The inclination determined from a single sample is thus representative of a partially time-averaged geomagnetic field. To ensure that SV is fully averaged along with other sources of noise, we compute mean paleolatitudes from groups of samples that span 50-100 m of drilling depth. The best estimates come from correcting this mean for a bias that arises because the geomagnetic polarity of azimuthally unoriented drill cores is unknown in some cases. We refer to this as the polarity ambiguity (POAM) bias (described below).
Basalt samples from a single flow only give an instantaneous measure of the geomagnetic field. In some cases, multiple flows may be extruded within such a short time interval that they only provide redundant samples of the same instant of geomagnetic field variation. To average SV, generally more than ~10 independent samples of the field are considered sufficient. As shown below, the 30 m of basalts probably contain ~12 independent units. The best estimate of the paleolatitude from the basaltic basement comes from the mean of these 12 independent units, after correcting for the POAM bias
(Table 19, Table
20, Table 21).
Calculating Mean Paleolatitudes
We group the paleomagnetic inclinations by depth within each hole and then compute the mean paleolatitude for each depth range in two ways
(Table 21). In the first method (column labeled "A-Mean Paleolatitude" in
Table 21), we take the absolute value of inclinations for a group of samples, convert these to paleolatitudes, and then compute the mean. For example, there are 33 samples from 848 to 903 mbsf from Hole 998B, 16 with positive and 17 with negative inclinations. The mean paleolatitude from all 33 samples is 8.5°. In the second method (column labeled "B-Mean Paleolatitude" in
Table 21), we find the mean paleolatitude from all the samples with positive inclinations and the mean paleolatitude from the absolute value of all the samples with negative inclinations, and then average these two values. For the example from Hole 998B, the mean computed this way is 8.6°.
These "B-Mean" paleolatitudes are useful for assessing the effect of possible unremoved secondary components. Again, we use the 33 samples from 848 to 903 mbsf from Hole 998B as an example case. Comparison of the mean inclination of the samples with positive inclinations (21.9°) to the mean of those with negative inclinations (-10.7°), indicates that the drill-string overprint seen in the split-core results is probably also present in the discrete samples. The effect is what would be expected if a present-day and/or a drill-string overprint were present (i.e., the normal polarity directions would be biased toward steeper directions and the reversed polarity directions toward shallower). Assuming this overprint is present, then the size of the bias produced by the overprint, which can be estimated from the means, is ~5.6° [= (21.9° - 10.7°)/2] of inclination or ~2°-3° of paleolatitude. Because there are roughly equal numbers of samples with positive and negative inclinations, the bias is also canceled when the "A-Mean" paleolatitude is computed. If all the samples had the same sign, then the mean paleolatitude computed from them may have been biased by a few degrees.
In general, the means computed either way differ little because within each group there are similar numbers of samples with positive and negative inclinations. As discussed further below, because the sign of the inclination is not always indicative of the polarity of the sample, using the "B-Mean" paleolatitude may result in other biases. Also, using the "B-Mean" assumes that differences between the means of positive- and negative-inclination groups are related to secondary overprints rather than to a primary signal, which may not always be the case. We compute the "B-Mean" here only to illustrate the sense and size of possible secondary overprints on the paleolatitude estimates. On average, the "B-Mean" paleolatitude is only 0.6° less than the "A-Mean," and therefore, the effect of the overprint, if present, is negligible.
Our preferred mean paleolatitudes are the "A-Mean" paleolatitudes corrected for the POAM bias as discussed below.
Estimating Paleolatitudes from Azimuthally Unoriented Drill Cores with Shallow Inclinations
Estimating paleolatitudes from inclination data requires care as all estimators are biased and corrections need to be applied (Briden and Ward, 1966; Kono, 1980; McFadden and Reid, 1982; Cox and Gordon, 1984). The bias can be easily visualized for the case where the paleomagnetic pole and site lie at the same geographic point (i.e., the angular distance between the pole and the site, called the colatitude, is 0°). Consider a Fisherian distributed set of paleomagnetic poles about this mean. The angular distance between each of these poles and the mean pole gives a colatitude estimate, which will nearly always be >0°. We refer to this bias as the angular distance (AD) bias. The effect of the AD bias for paleolatitude studies is such that the mean, median, or other estimators of the colatitude will naturally be greater than the true colatitude of 0°. As discussed by Cox and Gordon (1984), the size of the bias (1) is large (comparable to the angular standard deviation of the observed colatitudes, which will be >8° for most paleomagnetic data sets) when the true paleolatitude is within a few degrees of the geographic poles; (2) is several degrees or more for latitudes >50°; (3) is less than ~0.5° within 25° of latitude of the equator; and (4) decreases to zero at the equator.
Thus, when analyzing inclination only data sets with shallow inclinations, the AD bias apparently should be very small or negligible. This generally is the case for the sedimentary units sampled here because the dispersion caused by SV is small and the Caribbean plate has been within 25° of the equator. The AD bias would likewise appear to be negligible for the basalt samples because they too must have formed within ~25° of the equator. This assumes, however, that the geomagnetic polarity of the rock sample from which the inclination was obtained is known, or at least that all rock samples have the same polarity.
For azimuthally unoriented drill cores from rock units that formed near the equator, determining the polarity of sedimentary units may be difficult and determining the polarity of basalt units nearly impossible. The polarity ambiguity arises for several reasons: (1) Because the cores are azimuthally unoriented, the declination cannot be used to determine polarity. (2) Because the inclination is shallow at or near the equator, the angular distance between reversed and normal polarity inclinations is small. (3) Because the paleomagnetic inclinations from any suite of rocks will have some degree of dispersion about their mean inclination, it is likely that when the mean inclination is shallow, the sign of the inclination will not be indicative of the polarity. This is particularly the case for extrusive igneous rocks, which typically have larger dispersion than sedimentary rocks. In this case, geomagnetic SV is large enough that within 20° of the equator both positive and negative inclinations would be expected for basalt flows formed during an interval of constant polarity. Basically, the sign of the inclination cannot be used as a definitive estimate of geomagnetic polarity.
The situation is less problematic for the sedimentary units because the dispersion is generally lower, and therefore, the sign of the inclination is more likely to reflect the polarity. Indeed, we were able to establish an accurate magnetostratigraphy for the interval from 217 to 396 mbsf at Site 1001, which spans Chron 27R to 31R (pp. 314-315 of Sigurdsson, Leckie, Acton, et al., 1997; V. Louvel and B. Galbrun, unpubl. data; King et al.,
Chap. 8, this volume). Even within these well-defined chronozones, the sign of the inclination is not always indicative of polarity. For example, the interval from 351 to 355 mbsf at Site 1001 is unambiguously part of Chronozone 29R. Within this interval, however, the inclination estimated from discrete samples is not always negative, but instead varies from - 9.6° to 1.1°. Unfortunately, we could not establish the magnetic polarity for the sedimentary units other than for the interval from 217 to 396 mbsf at Site 1001.
If the polarity is unknown and both polarities are present in a set of paleolatitude data, the average paleolatitude will be less than the true paleolatitude
(Fig. 7). Alternatively, if inclinations with negative values are assumed to have the opposite polarity as those with positive values, inverting the negative values (taking their absolute value) will produce a new set of paleolatitudes whose mean will be greater than the true paleolatitude. In either case, the bias can be as large or even larger than the AD bias noted in past studies.
We correct for the POAM bias using a method developed by G.D. Acton (unpubl. data). The correction is based on Monte Carlo simulations that use global SV models to predict the difference between true paleolatitudes and expected (observed) paleolatitudes. Here, we use Harrison's (1980) estimates of the precision parameter (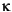 ) as a function of latitude for the basalts, which gives values of
) as a function of latitude for the basalts, which gives values of 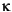
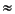 40 for near-equatorial sites (Fig. 8). We would expect that
40 for near-equatorial sites (Fig. 8). We would expect that 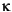 would be larger than this for the sedimentary units because each sedimentary sample partially averages SV. Indeed, using the method of McFadden and Reid (1982), we find that
would be larger than this for the sedimentary units because each sedimentary sample partially averages SV. Indeed, using the method of McFadden and Reid (1982), we find that 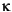 varies from 70 to 110 for subsets of data from the interval 217-396 mbsf at Site 1001 where the polarity is known. We therefore use
varies from 70 to 110 for subsets of data from the interval 217-396 mbsf at Site 1001 where the polarity is known. We therefore use 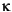 = 80 as a representative value for the sedimentary intervals where the polarity is unknown.
= 80 as a representative value for the sedimentary intervals where the polarity is unknown.
The method works as follows:
- Generate a set of N (typically 10,000 in this study) Fisherian distributed virtual geomagnetic poles (VGPs) about a known pole location (the north pole) and with a known dispersion.
- Compute the inclinations that would be observed at a site with known latitude from each of the N VGPs. Repeat this at sites going from 0° to 90° latitude at increments of 0.1°.
- Take the absolute values of the inclinations and convert these to a set of paleolatitudes.
- Compute the mean paleolatitude at each synthetic site. This is the expected paleolatitude (i.e., what one would expect to observe from a real data set). An example table is shown for
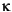 = 40 and 80, N = 10,000, and for known paleolatitudes of 0°-90° (Table
19). From this table, it is clear that we expect to get a value that is biased away from the equator (i.e., the expected paleolatitude is larger than the true paleolatitude). The difference between the expected and the true paleolatitudes gives the bias correction, T.
= 40 and 80, N = 10,000, and for known paleolatitudes of 0°-90° (Table
19). From this table, it is clear that we expect to get a value that is biased away from the equator (i.e., the expected paleolatitude is larger than the true paleolatitude). The difference between the expected and the true paleolatitudes gives the bias correction, T.
- Take the absolute values of the observed inclinations, convert these to paleolatitudes, and then compute a mean paleolatitude (
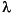 mean). Compare this value to the expected values determined from the Monte Carlo simulations in
Table 19. The true paleolatitude (
mean). Compare this value to the expected values determined from the Monte Carlo simulations in
Table 19. The true paleolatitude (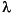 true), corresponds to the unbiased estimate of the paleolatitude (
true), corresponds to the unbiased estimate of the paleolatitude (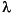 unbiased) for the real data. The relationships are
unbiased) for the real data. The relationships are
-
T(
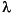 exp) =
exp) = 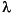 exp -
exp - 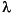 true
true 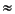 T(
T(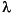 mean) and (1)
mean) and (1)
-
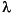 unbiased =
unbiased = 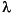 mean - T
mean - T 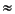
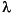 true, (2)
true, (2)
where T(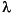 exp) refers to the bias correction at an expected paleolatitude of
exp) refers to the bias correction at an expected paleolatitude of 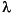 exp. For example, if we compute an observed mean paleocolatitude of 8°, the unbiased paleolatitude would be 4.5° assuming
exp. For example, if we compute an observed mean paleocolatitude of 8°, the unbiased paleolatitude would be 4.5° assuming 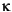 = 40 and using Table 19. The bias correction, T(8°), is 3.5° in this case. This bias correction includes both the AD and POAM biases, though the former is negligible for Caribbean data.
= 40 and using Table 19. The bias correction, T(8°), is 3.5° in this case. This bias correction includes both the AD and POAM biases, though the former is negligible for Caribbean data.
The uncertainty calculation for the unbiased paleolatitude follows from that given by Cox and Gordon (1984, pp. 56-57). We define ST as the best estimate of total standard error in the paleolatitude, where
-
ST2 = SR2 + SS2 . (3)
SR is the standard error attributed to random errors in the paleolatitudes and SS is the standard error attributed to systematic errors. These are all univariate standard errors. Just like the mean paleolatitude, the value of SR can be biased by the polarity ambiguity. It must therefore be estimated either from the dispersion of the paleolatitudes or from the value expected from SV. We define SSV as the standard error expected owing to SV, and SB as the between-flow standard error for basalts or the between-sample standard error for sediments. For N independent samples of the geomagnetic field, SSV = 81°/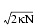 . SB is estimated from the dispersion of the paleolatitudes. We then take SR to be the larger of SSV or SB. We assign SS a value of 2° to account for systematic errors, such as those resulting from deviation of the drill hole from vertical. The upper S(+) and lower S(-) bounds for the standard error of the unbiased paleolatitude are then given by
. SB is estimated from the dispersion of the paleolatitudes. We then take SR to be the larger of SSV or SB. We assign SS a value of 2° to account for systematic errors, such as those resulting from deviation of the drill hole from vertical. The upper S(+) and lower S(-) bounds for the standard error of the unbiased paleolatitude are then given by
-
S(-) =
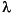 mean - ST - T(
mean - ST - T(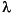 mean - ST), (4)
mean - ST), (4)
with the restriction that S(-) 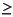 0, and
0, and
-
S(+) =
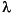 mean + ST - T(
mean + ST - T(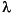 mean + ST). (5)
mean + ST). (5)
The error bounds are restricted to positive paleolatitudes because we are analyzing the absolute values of the inclinations. For our example case with 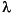 mean and
mean and 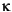 = 40, lets assume that ST is 3.3°. Then S(-) = 8.0° - 3.3° - T(8.0° - 3.3°) = 8.0° - 3.3° - 7.2°, but because S(-) must be
= 40, lets assume that ST is 3.3°. Then S(-) = 8.0° - 3.3° - T(8.0° - 3.3°) = 8.0° - 3.3° - 7.2°, but because S(-) must be 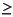 0, the best estimate of the lower bound is 0.0°. Similarly, S(+) = 8.0° + 3.3° - T(8.0° + 3.3°) = 8.0° + 3.3° - 1.0° = 10.3°. The unbiased mean lies between 0° and 10.3°, which is denoted here as
0, the best estimate of the lower bound is 0.0°. Similarly, S(+) = 8.0° + 3.3° - T(8.0° + 3.3°) = 8.0° + 3.3° - 1.0° = 10.3°. The unbiased mean lies between 0° and 10.3°, which is denoted here as 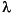 unbiased = 4.5° (+5.8° or -4.5°; 1
unbiased = 4.5° (+5.8° or -4.5°; 1 ). The 95% confidence limits are similarly calculated except that ST is replaced by 1.96 ST in equations 4 and 5.
). The 95% confidence limits are similarly calculated except that ST is replaced by 1.96 ST in equations 4 and 5.

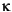 ) as a function of latitude for the basalts, which gives values of
) as a function of latitude for the basalts, which gives values of 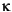
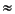 40 for near-equatorial sites (Fig. 8). We would expect that
40 for near-equatorial sites (Fig. 8). We would expect that 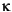 would be larger than this for the sedimentary units because each sedimentary sample partially averages SV. Indeed, using the method of McFadden and Reid (1982), we find that
would be larger than this for the sedimentary units because each sedimentary sample partially averages SV. Indeed, using the method of McFadden and Reid (1982), we find that 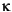 varies from 70 to 110 for subsets of data from the interval 217-396 mbsf at Site 1001 where the polarity is known. We therefore use
varies from 70 to 110 for subsets of data from the interval 217-396 mbsf at Site 1001 where the polarity is known. We therefore use 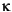 = 80 as a representative value for the sedimentary intervals where the polarity is unknown.
= 80 as a representative value for the sedimentary intervals where the polarity is unknown.
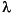 mean). Compare this value to the expected values determined from the Monte Carlo simulations in
mean). Compare this value to the expected values determined from the Monte Carlo simulations in
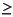 0, and
0, and
 ). The 95% confidence limits are similarly calculated except that ST is replaced by 1.96 ST in equations 4 and 5.
). The 95% confidence limits are similarly calculated except that ST is replaced by 1.96 ST in equations 4 and 5.