LABORATORY MEASUREMENTS
Crack porosity, composition, density, alteration, and mineral orientation are the most important factors responsible for significant variations in seismic velocities. A comparison between downhole logs and laboratory physical properties measurements obtained at atmospheric pressure shows a favorable correlation between the two types of data (Fig. F4). This correspondence is mainly attributed to the newer generation of logging tools (Dick, Natland, Miller, et al., 1999) used during Leg 176 for the downhole measurements and the higher data quality produced. In spite of these results, velocities at in situ pressures are often quite different from measurements at atmospheric pressure (Birch, 1960; Iturrino et al., 1991); therefore, it is important that velocity data used for crustal studies be obtained at elevated pressures. For example, seismic anisotropy can originate from either preferred mineralogical alignments or structural features.
For this study, compressional wave (VP) and shear wave (VS) velocities were measured at the New England Research Laboratories (see "Appendix") using the pulse transmission method (Birch, 1960; Christensen, 1965, 1985) under hydrostatic conditions up to confining pressures of 200 MPa. The upper pressure limit was chosen because previous experiments on Leg 118 samples (Iturrino et al., 1991) have shown that this upper limit minimizes the effects of cracks on velocities by closing the intergranular pore spaces and fracture openings, thus giving information on preferred mineral orientation in the oceanic crust. In many cases, microcracks develop by releasing the in situ stresses when the samples are brought to the surface from deep crustal sections (Iturrino et al., 1995). The 200-MPa limit also equates to the approximate in situ pressure of the lower oceanic crust in a more traditional 6-km section. VP , VS, and seismic attenuation measurements from core data are presented in Table T1, and the methods are described in "Appendix."
A comparison between atmospheric pressure compressional wave velocity values and in situ pressure measurements show some discrepancies. For this comparison, only measurements made in the same samples were used, in situ pressures were estimated from the effect of the water column, changes in pressure with depth due to the overburden rock column were estimated, and velocity values between velocity vs. pressure intervals were interpolated. In most instances, atmospheric pressure measurements display higher velocity values than those obtained from high-pressure measurements (Fig. F5A). Common measurements made in the upper 500 m (48 total samples) show that the average compressional wave velocity at atmospheric pressure is 6760 ± 387 m/s, whereas the average VP for the in situ measurements is 6602 ± 279 m/s. Below 500 m, the average VP at atmospheric pressure for eight samples is 6659 ± 212 m/s and 6820 ± 154 m/s for the in situ pressure measurements. Velocity discrepancies in the upper 500 m of the hole may be due to (1) difficulties in picking first arrivals on deformed and altered samples at atmospheric pressures, where in many cases, the first break is not sharp and may lead to earlier time picks or (2) a faulty calibration of the old velocity system used during Leg 118. Below 600 m, the atmospheric pressure velocity values seem to be more reliable as they are lower than in situ measurements. A comparison of the in situ pressure compressional wave velocity (Fig. F5B) and shear wave velocity measurements (Fig. F5C) with log data in the upper 600 m shows a better correlation between the two types of data. A compressional wave velocity gradient for the entire set of in situ measurements is defined by
-
VP = 6554.5 + 0.24833d with R = 0.34,
where d represents the depth in mbsf.
As with all shallow oceanic drill holes, fracture porosity is a major factor influencing the velocity structure of Hole 735B. Compressional wave velocity measurements obtained at low pressures indicate that there is a decrease in seismic velocities with increasing crack porosity for the gabbros of Hole 735B (Fig. F6A). However, compressional wave velocities do not show a strong relationship for porosity values >1%. The samples from Leg 176 do not show as large a range in porosities as the samples from shallower in the section, possibly because of bias sampling, or more likely, because porosity generally decreases with depth. However, velocities are still significantly affected by the closure of microcracks as the velocity vs. pressure data indicate (Table T1). Shear wave velocity measurements show that porosity has a similar effect on VS (Fig. F6B); however, the overall result is diminished and the differences may be due to structural influences as previously described (Iturrino et al., 1991).
Anisotropy is becoming more important in the interpretation of oceanic seismic data (Shor et al., 1973; Stephen, 1981; White and Whitmarsh, 1984; Shearer and Orcutt, 1985, 1986). For this study, variations in compressional wave velocities and shear wave splitting are examined in detail. In ideal cases, there are two simple styles of alignment in earth materials (horizontal and vertical), and laboratory studies suggest that they give rise to two types of anisotropy. In the horizontal style, or layered case, elastic properties may vary vertically, such as from layer to layer, but not horizontally. Such a material is called transversely isotropic with a vertical axis of symmetry. Waves generally travel faster horizontally, along layers, than vertically. The simplest case of the second type of anisotropy corresponds to a material with aligned vertical weaknesses such as cracks or fractures, or with unequal horizontal stresses. Elastic properties vary in the direction crossing the fractures but not along the plane of the fracture. Such a material is called transversely isotropic with a horizontal axis of symmetry or azimuthal anisotropy. Waves traveling along the fracture direction (but within the competent rock) generally travel faster than waves crossing the fractures.
Laboratory velocity measurements can assess the effects of both types of symmetry on anisotropy by careful sampling along the orientations of planes of weakness (see "Appendix"), especially when shear waves are measured. However, in a borehole, the maximum shear wave splitting is controlled by transverse isotropy with a horizontal axis of symmetry although, as in most cases with dipping structures, anisotropy can still result from a nonhorizontal symmetry axis where a maximum anisotropy could not be obtained. In the sections below, an assessment of compressional wave velocity anisotropy and shear wave splitting is provided for laboratory and downhole measurements.
Compressional Wave Velocities
The core samples from Leg 176 have a mean compressional wave velocity of 7036 ± 161 m/s measured at 200 MPa. This value is higher than the 6895 ± 307 m/s mean value of the upper 500 m of Hole 735B (Iturrino et al., 1991). The consistently higher compressional wave velocity values below 500 m correspond to a general decreasing trend in alteration with depth (Dick, Natland, Miller, et al., 1999) as well as a decrease in Fe-Ti oxides and the abundance of olivine gabbros (Fig. F2).
Even though most oceanic rocks contain large percentages of highly anisotropic minerals, they tend to be isotropic or nearly isotropic because of the random orientation of their main mineral constituents. Velocities for a mineral aggregate with a random orientation can be calculated from the minerals' elastic constants. Voigt (1928) and Reuss (1929) averages assume uniform strain and stress, respectively, and give high and low limits for the aggregate velocity. Commonly, the Voigt-Reuss-Hill average (VRH), which is the mean of the Voigt and Reuss averages (Hill, 1952), is used as the velocity for a monomineralic rock with random mineral orientation (Birch, 1961). The gabbros of Hole 735B with random mineral orientation should fall in a triangular field defined by the VRH averages of the main mineral constituents.
A velocity-density plot at 200 MPa, shown in Figure F7A, indicates that the seismic properties of most of the samples from Hole 735B fall in a region controlled by the VRH averages for plagioclase (An56), olivine, hornblende, and augite (Christensen, 1982). The samples that fall outside of these limits are those which show the highest degree of deformation at the top of the section (Iturrino et al., 1991). At 200 MPa, Leg 176 samples show a very small amount of VP anisotropy that ranges from 0.4% to 8.8%, with the majority of the samples having values less than 3.8% (Table T1). Compressional wave velocities were measured twice in the sample having the highest degree of VP anisotropy (176-735B-142R-3, 86-88 h´) and the results show a variation in anisotropy between 5.9% and 8.8%. Compositional variations between the individual samples from this core may explain the fact that velocity anisotropy is high while the samples plot within the VRH area defined by the main mineral constituents. This is evident by the 0.1 g/cm3 density difference between the samples (Table T1). Alteration can also cause deviations from the field defined by the VRH averages that will not be related to intrinsic anisotropic properties. Some of the samples from Leg 176 have a high degree of background alteration. However, in the majority of the cases, olivine and clinopyroxene are replaced by amphibole, and plagioclase is recrystallized as secondary plagioclase (Dick, Natland, Miller, et al., 1999). Therefore, the velocities from the main alteration mineral constituents should fall close within the limits defined by the VRH averages. Most of these results, in combination with thin section examinations of samples found in Units II through Unit XII, show either weak plastic deformation or random mineral orientation with distinct igneous textures (Dick, Natland, Miller, et al., 1999). Thus, these observations imply that there is no pervasive mineral orientation that would cause significant VP anisotropy especially below 600 mbsf. These results differ from ophiolite studies where gabbros with abundant olivine show a strong preferred mineral orientation (Christensen, 1978; Salisbury and Christensen, 1978).
Most of the laboratory shear wave measurements fall in a similar VRH field defined by plagioclase, olivine, hornblende, and augite (Fig. F7B). However, when compared to the VP vs. density plot, there is a shift to the field mostly dominated by plagioclase, hornblende, and augite. This shift may be due to either a lack of abundant VRH data that will constrain the VS limits or to other factors besides compositional variations affecting VS. Without complete thin section and chemical analyses, it is difficult to determine which one is the case. However, most of the Leg 176 samples have low VS anisotropy values (Table T1), suggesting that they should fall within a field defined by the main mineral constituents. Samples that fall outside this field are mainly from the top of Hole 735B, where up to 7% VS anisotropy has been previously recorded (Iturrino et al., 1991). In most cases, the VS anisotropy was caused by a large degree of deformation in mylonitic zones (Fig. F8). Only one of the Leg 176 samples shows significant shear wave splitting (176-735B-142R-3, 86-88, h´). This sample does not have any visible fabric, but it is short, has a high velocity value, and contains large crystals that are nearly the length of the sample itself. Grain size may very well explain these variations in VS as well as the observed VP anisotropy.
Seismic wave attenuation (Q-1) is a measure of the energy lost in a propagating wave through the conversion to frictional heat, also known as intrinsic attenuation, and extrinsic effects such as scattering. Intrinsic effects are generally attributed to loss of energy that decays exponentially in both frequency and propagation distance due to intergranular fluid flow associated with the propagation of an elastic wave (Kuster and Toksöz, 1974; Toksöz et al., 1979; Wepfer and Christensen, 1989; Goldberg et al., 1992). Scattering losses are the result of formation heterogeneities (Aki and Richards, 1980; Richards and Menke, 1983).
Computed values of QP , QS1, and QS2 for each sample are presented in Table T1 for compressional waves and two orthogonal shear waves (S1 and S2). Computations were performed following the method of Toksöz et al. (1979) and are briefly described in "Appendix." The results are reported for increasing confining pressures of 60, 100, 150, 200 MPa and a decreasing pressure interval of 60 MPa. Overall, most of these results fall within the range of previously reported values obtained at Hole 735B from laboratory and logging data (Goldberg et al., 1991, 1992; Swift and Stephen, 1992). Leg 176 samples with Q 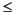 100 at 200 MPa have a mean QP value of 35.1 ± 20.1 (Table T2) compared to values of 32 ± 29 from previous laboratory work (Goldberg et al., 1991, 1992). Q values calculated from analyses of spectral ratios and amplitude decay on seismograms from the VSP experiment performed during Leg 118 range from 3 to 26 (Swift and Stephen, 1992). The values of QS1 and QS2 have averages of 22 ± 12.7 and 21 ± 7.9 (Table T2).
100 at 200 MPa have a mean QP value of 35.1 ± 20.1 (Table T2) compared to values of 32 ± 29 from previous laboratory work (Goldberg et al., 1991, 1992). Q values calculated from analyses of spectral ratios and amplitude decay on seismograms from the VSP experiment performed during Leg 118 range from 3 to 26 (Swift and Stephen, 1992). The values of QS1 and QS2 have averages of 22 ± 12.7 and 21 ± 7.9 (Table T2).
The agreement with the previously reported laboratory and log values from the top of the hole (Goldberg et al., 1991, 1992; Swift and Stephen, 1992) suggests that there is a general uniform trend in Q for this entire 1500-m section of lower oceanic crust. This is further emphasized by the QP values from 1497 mbsf, which range from 8.5 to 23.5 (Table T1). Overall, the Leg 176 samples also show a general trend of increasing Q with confining pressure (Table T1), suggesting that the closure of microcracks is influencing the overall attenuation values. Some of the samples within an individual core exhibit a large amount of QP anisotropy between vertical and horizontal measurements that do not necessarily correspond to large variations in velocity or QS (Fig. F9). In addition, several samples have Q values greater than 100. These values may indicate some variations with depth; however, some degree of caution should be used particularly when measuring Q in short and fast samples such as these. The procedure assumes that losses and waveform distortions due to geometric spreading and coupling between the sample and core-holder are identical for the reference material and each sample. Potentially significant problems arise due to variations in sample length and impedance, as well as poorly understood coupling phenomena, which are observed to be pressure dependent even for high Q standards such as aluminum. Observed amplitude spectra are also not always consistent with the underlying assumption of a constant Q material because of evidence of significant disruption of the waveforms due to scattering and sample heterogeneities.

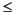 100 at 200 MPa have a mean QP value of 35.1 ± 20.1 (Table T2) compared to values of 32 ± 29 from previous laboratory work (Goldberg et al., 1991, 1992). Q values calculated from analyses of spectral ratios and amplitude decay on seismograms from the VSP experiment performed during Leg 118 range from 3 to 26 (Swift and Stephen, 1992). The values of QS1 and QS2 have averages of 22 ± 12.7 and 21 ± 7.9 (Table T2).
100 at 200 MPa have a mean QP value of 35.1 ± 20.1 (Table T2) compared to values of 32 ± 29 from previous laboratory work (Goldberg et al., 1991, 1992). Q values calculated from analyses of spectral ratios and amplitude decay on seismograms from the VSP experiment performed during Leg 118 range from 3 to 26 (Swift and Stephen, 1992). The values of QS1 and QS2 have averages of 22 ± 12.7 and 21 ± 7.9 (Table T2).