METHODS
During ODP Leg 204, sonic logs were recorded with the Schlumberger Dipole Sonic Imager (DSI) in six holes across southern Hydrate Ridge (Fig. F1). One monopole source and two dipole sources were used to generate the VP and the shear velocity (VS) logs, respectively. Full waveforms were recorded by the eight-receiver array for each source type. Because of the poorly consolidated nature of the sediments, compressional velocities are very close to the borehole fluid velocity and complete postcruise reprocessing of the monopole waveforms was necessary to discriminate properly the different arrivals and draw accurate VP logs. Because the DSI was not originally configured for such slow sediments, all the velocity logs were anomalously erratic at the time of the acquisition (see Tréhu, Bohrmann, Rack, Torres, et al., 2003). We used the slowness-time coherence (STC) processing method (Kimball and Marzetta, 1984; Harrison et al., 1990) to reprocess all the waveforms recorded.
In the STC method, a fixed-length window is moved along the first receiver waveform in discrete overlapping time step within a range of possible arrival times. For each time step, the window is moved linearly across the different receivers, the moveout between receivers corresponding to a given velocity, or, more accurately, slowness value. For each time step, the slowness value is then varied in discrete velocity increments within a predefined range. For each time and slowness step, a semblance function is calculated within the time window across the receiver arrays (Kimball and Marzetta, 1984). The peaks in semblance, or in coherence, are assumed to correspond to individual mode arrivals. The method can be refined by constraining accurately the probable arrival times and velocity ranges and by reducing the time and velocity steps. The STC processing routine used was part of the Schlumberger GeoFrame software.
For each hole, we show the results of the STC analysis of all the sonic logging waveforms recorded. The color in these figures represents the projection of the STC plane on the slowness axis. Two logging passes were made in each hole, making it possible to use different source frequencies between passes and thus to investigate the influence of the source frequency on the waveforms in the presence of gas hydrate. The central frequencies used for the monopole source were a "standard" frequency of ~12.5 kHz and a lower frequency of ~6.0 kHz. Unless otherwise indicated on the corresponding figure, the central frequencies of the dipole sources were ~800 Hz for the lower dipole and ~2.0 kHz for the upper dipole. Whereas the amplitude and the character of the recorded waveforms are different depending on the nature and frequency of the acoustic sources, reflecting a possible influence of gas hydrate on the higher frequency waveforms for the dipole, the figures show that, for each hole, the STC results were similar between passes. However, these figures also show that in most cases the lower frequency sources generated a higher coherence across the receiver array and resulted in more robust velocity logs. Consequently, we use only the velocity logs generated with the lower frequency sources in the subsequent analysis of the data, the generation of synthetic seismograms, and the estimation of gas hydrate and free gas saturations.
The generation of synthetic seismograms is a widely recognized method to tie borehole data with seismic surveys (Peterson et al., 1955; Wuenschel, 1960). The VP and the density ( ) wireline logs are used to calculate seismic impedance (
) wireline logs are used to calculate seismic impedance ( VP) and generate a reflection coefficient series. The velocity log is integrated into cumulative transit time in order to translate the reflection coefficient series into the time domain. For each hole, a synthetic wavelet was extracted from the 3-D seismic survey by statistical correlations between the seismic traces closest to the borehole location. The synthetic seismogram was then calculated by convolution of the wavelet with the reflection coefficient series. Finally, the resulting synthetic seismograms were tied with the seismic data by identifying the strongest reflectors at the different sites, such as the BSR and Horizons A, B, and B´. We used the IESX seismic integration module of the Schlumberger/GeoQuest GeoFrame software to generate the synthetic seismograms and to integrate the logging data within the 3-D seismic survey.
VP) and generate a reflection coefficient series. The velocity log is integrated into cumulative transit time in order to translate the reflection coefficient series into the time domain. For each hole, a synthetic wavelet was extracted from the 3-D seismic survey by statistical correlations between the seismic traces closest to the borehole location. The synthetic seismogram was then calculated by convolution of the wavelet with the reflection coefficient series. Finally, the resulting synthetic seismograms were tied with the seismic data by identifying the strongest reflectors at the different sites, such as the BSR and Horizons A, B, and B´. We used the IESX seismic integration module of the Schlumberger/GeoQuest GeoFrame software to generate the synthetic seismograms and to integrate the logging data within the 3-D seismic survey.
Vertical Seismic Profiles
Intermediate in scale and resolution between the sonic logs and the 3-D seismic data, the VSP surveys undertaken during Leg 204 were primarily aimed at defining the gas hydrate distribution on Hydrate Ridge and refining the signature of gas hydrate in the seismic data. They were also used to derive independent TvD relationships that could be used to tie the well data with the seismic data and to calibrate similar relationships derived from the synthetic seismograms. The detail of the operations and a complete description of the tools and methods used is given by
Tréhu et al. (this volume).
VSP surveys were attempted at five sites. Because of operational difficulties, only the surveys in Holes 1247B, 1250F, and 1244E were successful in recording coherent waveforms at multiple closely spaced stations. Despite attempts at multiple depths in Hole 1251H, only four stations offered sufficient coupling between the tool and the formation to record clear arrivals. We show the stacked waveforms recorded at all the successful stations in these holes in Figures F2, F3, F4, and F5. The waveforms in these figures have not been corrected for the position of the source and the triggering delay, and the traveltime is not the actual transit time used in the TvD relationship. The sharpness of the first arrivals is an indication of the strength of the coupling between the tool and the formation and consequently of the quality of the data. The correct identification of the first arrivals in Holes 1244E, 1247B, and 1250F allowed us to calculate interval velocity values that could be compared with the VP logs in these wells. Assuming that the wave path is vertical, the interval velocity between two stations is calculated by dividing the depth span between them by the difference in the first arrival transit times. The resulting velocity is assigned to the middle depth between the two stations. In the figures for the results in Holes 1244E and 1247B, the results have been smoothed by a five-sample moving average window.
Identification of Gas Hydrate from Elastic Properties
The commonly observed increase in sonic velocity in the presence of gas hydrate can be understood intuitively by the replacement of the pore fluid by the solid crystalline structure of methane clathrates. However, this simple substitution process is not sufficient to generate the increase in sonic velocity observed, most significantly in shear velocity. Although the purpose of this work is not to compare the merits of the various models existing to estimate gas hydrate saturations from sonic logs, it is necessary to provide an estimate of the gas hydrate saturations that can be associated with the various attributes of the sonic logs discussed.
Guerin et al. (1999) and Guerin and Goldberg (2005) show that some degree of cementation of the sediment grains by gas hydrates must occur to generate the increases in VP and VS observed in hydrate-bearing sediments. Guerin et al. (1999) conclude that, among other models, the best description of the elastic properties of the Blake Ridge gas hydrate–bearing sediments is the cementation theory of Dvorkin and Nur (1996), assuming that hydrate is deposited uniformly on the grains. In this formulation, the effect of cementation on the elastic properties is measured by the dry bulk modulus of randomly packed identical grains with interstitial cement (Dvorkin et al., 1994). The dry sediments/hydrate frame is
-
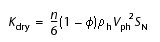 , (1)
, (1)
where
n = number of contact points between grains (assumed to be 9),
 = sediment porosity,
= sediment porosity,
 h = density, and
h = density, and
Vph = compressional velocity of gas hydrate (Dvorkin and Nur, 1996).
The normal stiffness SN is proportional to the stiffness of a cemented two-grains combination. It depends on the amount of cement (i.e., on the gas hydrate saturation S) on the cement/grain configuration and on the elastic properties of gas hydrate and of the grains. A statistical formulation, assuming that gas hydrate is deposited uniformly on the grains, was derived by Dvorkin and Nur (1996):
-
SN = AN
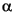 2 + BN
2 + BN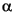 + CN, with (2)
+ CN, with (2)
-
AN = –0.024153
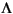 N–1.3646, (3a)
N–1.3646, (3a)
-
BN = 0.20405
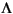 N–0.89008, (3b)
N–0.89008, (3b)
-
CN = 0.00024649
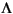 N–1.9846, (3c)
N–1.9846, (3c)
-
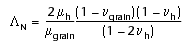 , and (4)
, and (4)
-
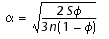 , (5)
, (5)
where
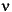 grain = Poisson's ratio of the grain, and
grain = Poisson's ratio of the grain, and
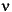 h = Poisson's ratio of gas hydrate,
h = Poisson's ratio of gas hydrate,
-
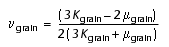 , and (6a)
, and (6a)
-
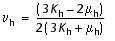 , (6b)
, (6b)
where
Kgrain = bulk modulus of the grain,
µgrain = shear modulus of the grain,
Kh = bulk modulus of the gas hydrate, and
µh = shear modulus of the gas hydrate.
Assuming that the Hydrate Ridge sediments are a mixture of sand and shale, if 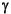 is the volumetric shale fraction, the grain moduli can be estimated by a Voigt-Reuss-Hill average of the moduli of sand and clay:
is the volumetric shale fraction, the grain moduli can be estimated by a Voigt-Reuss-Hill average of the moduli of sand and clay:
-
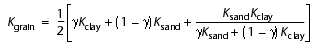 , (7a)
, (7a)
and
-
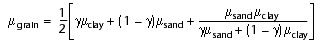 . (7b)
. (7b)
Knowing from core analysis the actual range of sand and shale fractions for each site, we use a normalized gamma ray log to calculate 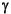 .
.
According to Gassmann (1951), the in situ dry modulus of the sediments can be calculated from the measured in situ bulk modulus K by
-
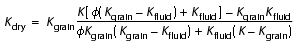 , (8)
, (8)
where
Kgrain = sediment grain bulk modulus and
Kfluid = pore fluid bulk modulus.
K can be derived from the velocity and the density logs:
-
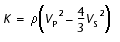 . (9)
. (9)
Using the velocity, density, and porosity logs and assuming that the pore fluid is only seawater, we use Equation 9 to calculate the in situ bulk modulus from the logs and Equation 8 to derive the dry bulk modulus of the Hydrate Ridge sediments. Starting from purely water-saturated sediments, we then increase hydrate saturation (S) in the expression of SN (Equations 2–5) until the theoretical dry bulk modulus calculated with Equation 1 matches the measured dry bulk modulus. The values of the different parameters are given in Table T1.
Below the BSR, the possible presence of free gas is indicated qualitatively by significantly lower VP values. The saturation of free gas in the pore space can be calculated by fluid substitution in the Biot/Gassmann model (Gassmann, 1951; Murphy, 1984). In this model, the expression for the bulk modulus, from which Equation 8 is derived, is
-
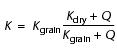 , with (10a)
, with (10a)
-
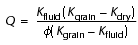 . (10b)
. (10b)
Without knowledge of the fluid bulk modulus, which depends strongly on the unknown free gas saturation, one has to use a theoretical formulation to determine the dry frame modulus. Dvorkin et al. (1999) studied the effect of consolidation on the elastic properties of dry marine sediments and defined two regimes depending whether porosity is above a critical value ( c, usually 36%–40%). If porosity is above
c, usually 36%–40%). If porosity is above  c, which is the case in all sites drilled on Hydrate Ridge where porosities are consistently above 40%, the dry modulus is
c, which is the case in all sites drilled on Hydrate Ridge where porosities are consistently above 40%, the dry modulus is
-
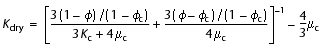 , (11)
, (11)
where
Kc = dry bulk modulus at the critical porosity, and
µc = shear modulus at the critical porosity,
-
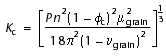 , and (12a)
, and (12a)
-
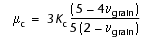 , (12b)
, (12b)
where
n = average number of grain contacts per grain (previously assumed
to be 9), and
P = effective pressure.
If Sgas is the free gas saturation, the pore fluid bulk modulus can be estimated by a weighted average of the bulk moduli of the two phases present in the pore space (Murphy, 1984):
-
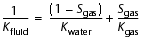 . (13)
. (13)
A simple manipulation of Equation 10 provides an expression for Kfluid as a function of the saturated (K) and dry (Kdry) bulk moduli, which are derived, respectively, from the velocity and density logs (Equation 9) and from the porosity log (Equation 11). Sgas is then calculated from Kfluid by Equation 13.
Sonic Logging Waveform Amplitude
Guerin and Goldberg (2002) show that sonic logging waveforms display lower amplitudes in gas hydrate–bearing intervals. Empirical relationships and modeling of elastic wave propagation in hydrate-bearing sediments (Guerin and Goldberg, 2002; Guerin et al., 2005) suggest that the correlation between sonic attenuation and hydrate saturation is not strong enough to estimate qualitatively the low hydrate saturations (approximately <20%) typical of the intervals logged during Leg 204. However, the display of the waveform amplitudes alongside other logs provides a qualitative indicator of gas hydrate occurrence. Low amplitudes are also traditionally associated with the presence of free gas (Murphy, 1982) and can be observed in several intervals below the BSR on Hydrate Ridge.

 ) wireline logs are used to calculate seismic impedance (
) wireline logs are used to calculate seismic impedance ( VP) and generate a reflection coefficient series. The velocity log is integrated into cumulative transit time in order to translate the reflection coefficient series into the time domain. For each hole, a synthetic wavelet was extracted from the 3-D seismic survey by statistical correlations between the seismic traces closest to the borehole location. The synthetic seismogram was then calculated by convolution of the wavelet with the reflection coefficient series. Finally, the resulting synthetic seismograms were tied with the seismic data by identifying the strongest reflectors at the different sites, such as the BSR and Horizons A, B, and B´. We used the IESX seismic integration module of the Schlumberger/GeoQuest GeoFrame software to generate the synthetic seismograms and to integrate the logging data within the 3-D seismic survey.
VP) and generate a reflection coefficient series. The velocity log is integrated into cumulative transit time in order to translate the reflection coefficient series into the time domain. For each hole, a synthetic wavelet was extracted from the 3-D seismic survey by statistical correlations between the seismic traces closest to the borehole location. The synthetic seismogram was then calculated by convolution of the wavelet with the reflection coefficient series. Finally, the resulting synthetic seismograms were tied with the seismic data by identifying the strongest reflectors at the different sites, such as the BSR and Horizons A, B, and B´. We used the IESX seismic integration module of the Schlumberger/GeoQuest GeoFrame software to generate the synthetic seismograms and to integrate the logging data within the 3-D seismic survey.
 = sediment porosity,
= sediment porosity,
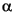 2 + BN
2 + BN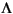 N–1.3646, (3a)
N–1.3646, (3a)
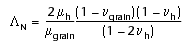 , and (4)
, and (4)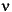 grain = Poisson's ratio of the grain, and
grain = Poisson's ratio of the grain, and
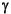 is the volumetric shale fraction, the grain moduli can be estimated by a Voigt-Reuss-Hill average of the moduli of sand and clay:
is the volumetric shale fraction, the grain moduli can be estimated by a Voigt-Reuss-Hill average of the moduli of sand and clay:
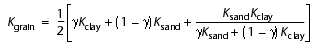 , (7a)
, (7a)
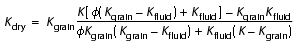 , (8)
, (8)
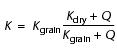 , with (10a)
, with (10a)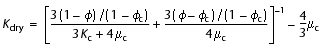 , (11)
, (11)
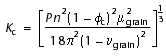 , and (12a)
, and (12a)